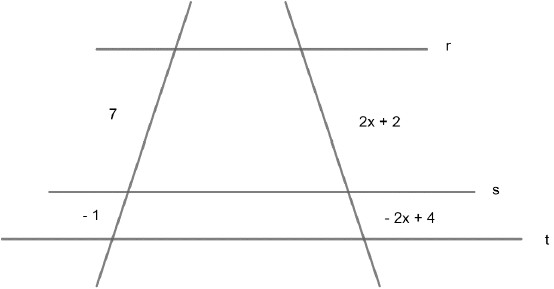
Considerando que r//s//t, ou seja, que as retas r, s e t são paralelas entre si, e analisando a imagem a seguir, pode-se afirmar que o valor de x é igual a:

FUNDATEC - 2023 - Analista Superior (CAU RS)/Sem Área

Considerando que r//s//t, ou seja, que as retas r, s e t são paralelas entre si, e analisando a imagem a seguir, pode-se afirmar que o valor de x é igual a:

2,5
–2,5
2,166...
–2,166...
1,625

Solução detalhada

Compreendendo o problema:

Temos três retas paralelas (r, s e t) cortadas por duas transversais. O objetivo é encontrar o valor de x, utilizando as informações sobre os segmentos de reta determinados pelas paralelas e transversais.

Aplicando o Teorema de Tales:

O Teorema de Tales estabelece que, quando retas paralelas cortam duas transversais, os segmentos correspondentes determinados nas transversais são proporcionais.

Montando a proporção:

Podemos montar a seguinte proporção utilizando os segmentos das transversais:

(2x + 2) / 7 = (-2x + 4) / (-1)

Resolvendo a equação:

Multiplicando cruzado:
- (-1)(2x + 2) = 7(-2x + 4)
- -2x - 2 = -14x + 28
Isolando o x:
- -2x + 14x = 28 + 2
- 12x = 30
Dividindo por 12:
- x = 30 / 12
- x = 2,5

Resposta:

O valor de x é 2,5.

Portanto, a alternativa correta é a primeira opção: 2,5.

Conclusão:

Utilizando o Teorema de Tales, conseguimos estabelecer uma proporção entre os segmentos de reta e, através da resolução da equação, encontramos o valor de x.

Observação: O Teorema de Tales é uma ferramenta fundamental para resolver problemas envolvendo retas paralelas e transversais, permitindo encontrar medidas de segmentos e estabelecer relações entre diferentes figuras geométricas.

JAMAL MALIK.