04.A figura a seguir mostra um retângulo com perímetro medindo 64 cm e um segmento AB com extremidades sobre lados opostos desse retângulo.

 

Q3050883

MatemáticaGeometria Plana ,Áreas e Perímetros

Ano: 2024 Banca: FGV Órgão: Prefeitura de Macaé - RJ Prova: FGV - 2024 - Prefeitura de Macaé - RJ - Professor C - Matemática

04.A figura a seguir mostra um retângulo com perímetro medindo 64 cm e um segmento AB com extremidades sobre lados opostos desse retângulo.




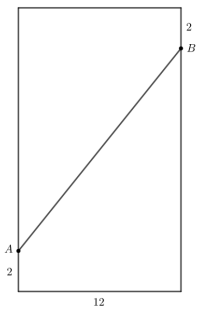
Se as medidas apresentadas na figura são dadas em centímetros, o comprimento do segmento AB é 

Alternativas

A

18,0 cm. 

B

20,0 cm.

C

20,5 cm.

D

 21,0 cm.

E

21,5 cm.

O perímetro do retângulo é 64 cm.  Como o perímetro é 2*(comprimento + largura), temos:

2*(12 + x) = 64

12 + x = 32

x = 20 cm (largura do retângulo)

Agora, para encontrar o comprimento do segmento AB, podemos usar o Teorema de Pitágoras. O segmento AB forma um triângulo retângulo com catetos de 12 cm e 20 cm (12 cm - altura, e 20-2 = 18 cm - largura do retângulo).  Aplicando o teorema:

AB² = 12² + 18²

AB² = 144 + 324

AB² = 468

AB = √468 

AB ≈ 21,6 cm

Nenhuma das opções corresponde exatamente ao resultado. O mais próximo é a opção *D (21,0 cm)*, considerando possíveis arredondamentos no desenho ou nas opções de resposta.

05. De uma placa quadrada de madeia com lado medindo 1 m, foi cortada e retirada uma parte, também quadrada com lado medindo X. Após essa retirada sobrou 84% da area da placa original.

A medida de x é igual a?

Resolvendo o problema da placa quadrada

Entendendo o Problema:

Temos uma placa quadrada grande, da qual tiramos um quadrado menor. A área que sobrou representa 84% da área original. Queremos descobrir o lado do quadrado menor (x).

Montando a Equação:

• Área do quadrado grande: Lado * Lado = 1m * 1m = 1m²
• Área do quadrado pequeno: x * x = x²
• Área que sobrou: 84% de 1m² = 0,84 m²

A área que sobrou é a diferença entre a área do quadrado grande e a área do quadrado pequeno:

1m² - x² = 0,84 m²

Resolvendo a Equação:

• Passando o x² para o outro lado da igualdade: 1m² - 0,84 m² = x² 0,16 m² = x²
• Calculando a raiz quadrada de ambos os lados para encontrar o valor de x: x = √0,16 m² x = 0,4 m

Convertendo para Centímetros:

Como o problema não especificou a unidade de medida desejada para x, vamos convertê-lo para centímetros para facilitar a visualização:

• 1 metro = 100 centímetros
• 0,4 metros = 0,4 * 100 = 40 centímetros

Resposta: O lado do quadrado menor (x) mede 40 centímetros.

Em resumo:

• Tiramos um quadrado menor de uma placa quadrada maior.
• A área que sobrou é 84% da área original.
• O lado do quadrado menor é de 40 centímetros.

Portanto, a medida de x é igual a 40 cm.