De onde vem o número de Euler

Como a matemática é essencial na área do machine learning e da ciência de dados, vale a pena aprender esse conceito. É possível que você já tenha escutado sobre esse assunto em vários locais diferentes e ainda não esteja entendendo de onde esse número vem e qual a utilidade dele.
Então, nosso objetivo aqui é explicar um pouco para vocês sobre a origem do número de Euler, para que ele serve e contar algumas curiosidades.
A origem do número de Euler
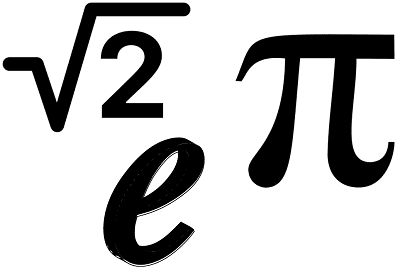
Ou seja, esses números vêm da geometria.
O número de Euler, entretanto é diferente, ele tem sua origem no conceito de taxa de juros.
Com base nisso, talvez você pense “eu não entendo nada de juros, isso vai ser muito complicado”. Calma! Vamos imaginar um exemplo e você vai ver que é tudo muito simples.
Pense que você deixou um valor na poupança durante um ano; depois de um ano, o banco irá pagar um rendimento, digamos de 100%. Esses 100% são a taxa de juros.
Observe que esse valor é irreal, nenhum banco paga um rendimento de 100%; entretanto, um número assim facilita nosso exemplo. Como calcularíamos quanto teremos ao final desse ano? Podemos utilizar a fórmula abaixo:

V é o valor que você terá no final de um ano; M é o montante inicial que você depositou; (1 + 1) é a porcentagem inicial (1) mais a taxa de juros (100% = 1).
Agora, vamos imaginar que o banco fez outra proposta: em vez de pagar ao final do ano 100% de uma vez, ele pagará metade dos juros em seis meses e outra metade quando fechar o ano.
Como representaremos isso em uma fórmula? Multiplicaremos o M pela metade dos juros e depois novamente por mais metade desses juros até fechar o ano. Confira abaixo:
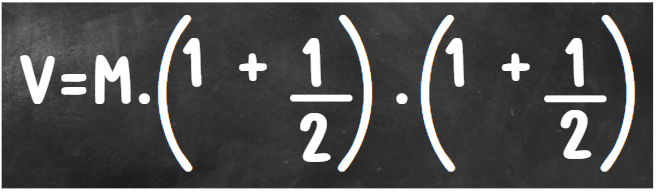
Lembre-se que essa fórmula também pode ser representada da seguinte forma V=M.(1+1/2)².
Qual dessas opções apresentadas acima é a melhor? Essa resposta independe do nosso valor investido. O que importa saber é o que é maior: (1+1) ou (1+1/2)²? O resultado de (1+1) é 2; o resultado de (1+1/2)² é 2,25.
Logo, a segunda opção é melhor; pois 2,25 é maior que 2. Assim, percebemos que é mais interessante receber um juro dividido em duas partes e multiplicado do que receber um juro inteiro em uma parte só. O valor final recebido será maior no segundo caso.
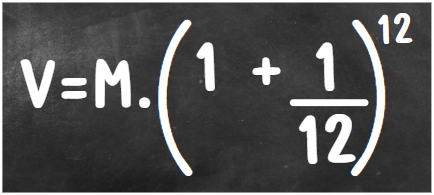
Mas, será que isso acontece sempre? Vamos imaginar que, agora, em vez de pagar os juros a cada seis meses, o banco irá pagar uma vez por mês; ou seja, o valor será pago em 12 vezes, conforme apresentado na fórmula ao lado.
No primeiro caso tínhamos um resultado de 2, no segundo um resultado de 2,25. Agora, você pode conferir com sua calculadora: o valor recebido será multiplicado por 2,61.
Dessa forma, é possível perceber que, quanto mais aumentamos as divisões, maior ficará o valor. Se considerarmos que o banco paga o valor por semana, teríamos um cálculo de (1+1/52)52 = 2,69; se fosse por dia, teríamos (1+1/365)365 = 2,71 e assim por diante.
Como vemos, o valor do expoente foi aumentando bastante: de 1 foi para 2, depois para 12, para 52 e, por fim, para 365. O resultado, entretanto, está subindo a uma taxa menor: primeiro tivemos 2, depois 2,25, 2,61, 2,69 e, então 2,71.
Quem estava analisando essa questão era Bernoulli – um matemático famoso – e ele percebeu que, quanto mais se aumentava o expoente, mais o resultado se aproximava de um limite; aparentemente, o resultado não cresceria para sempre.
Então ele formulou a seguinte questão: se o expoente fosse aumentado ao infinito, qual seria o resultado da equação? Matematicamente escrevemos isso como na imagem abaixo:
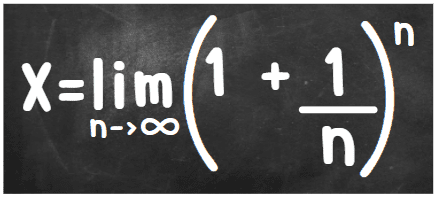
Nós lemos a equação da seguinte forma: qual seria o valor do limite de (1+1/n) elevado na “n” quando “n” tende ao infinito? Bernoulli não conseguiu chegar a uma resposta.
Quem responde isso, anos depois é Euler. Ele descobriu que o resultado dessa equação, quando “n” tendia para o infinito, dava o número 2,71828… Esse número, chamado de “e”, tem infinitos dígitos, mas é específico e estabelecido. Após isso, foi descoberto que esse número tem muitas aplicações.
Uma pequena curiosidade aqui. Alguns podem até pensar que Euler era egocêntrico e por isso escolheu dar a letra “e” para o número porque essa era a inicial de seu nome.
Entretanto, ao que tudo indica, a letra foi escolhida ao acaso; foi uma coincidência muito feliz porque acabou tornando-se, depois, um número extremamente importante que leva o nome e a letra inicial de seu descobridor.
Onde mais aparece o número de Euler?
O número de Euler também pode ser relacionado com fatoriais. Se você não lembra, fatoriais são representados com “pontos de exclamação” como 3!, 4!, 5! etc.
O fatorial 3! é 3x2x1, 4! é 4x3x2x1, 5! é 5x4x3x2x1 e assim por diante.
Se fizermos a seguinte soma 1+1/(1!)+1/(2!)+1/(3!)+1/(4!)+… até o infinito, teremos como resultado o número de Euler.
Matematicamente, dizemos que o número de Euler é igual ao somatório de 1/(n!), no qual “n” varia de 0 até o infinito.
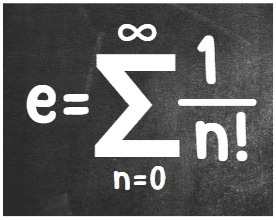
Um dos lugares mais fascinantes onde aparece o número de Euler é no gráfico de y = e x . Veja abaixo:
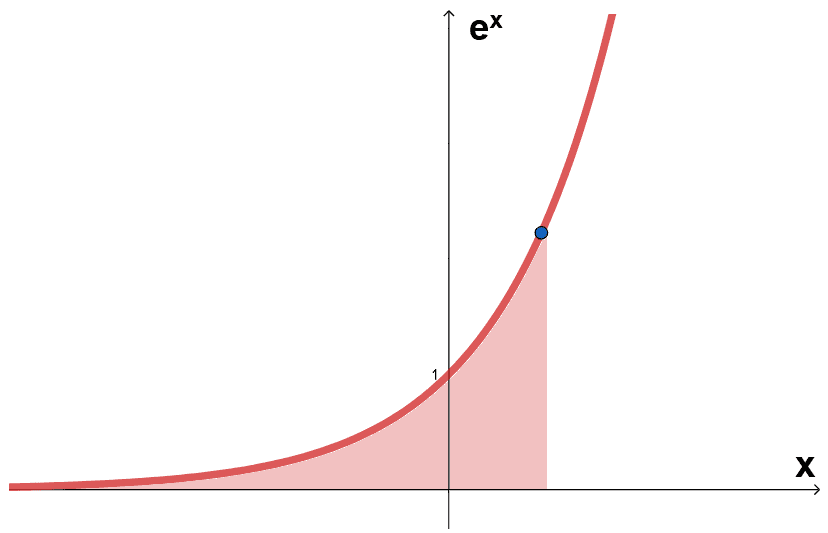
Esse gráfico é exponencial e a função corta o eixo y em 1, pois y elevado na 0 é 1. E por que essa função é especial?
Nessa função, em qualquer ponto aleatório que escolhermos, a inclinação da curva nesse ponto será igual a ex. Dessa forma, em um ponto em que x é igual a 9, por exemplo, a taxa de variação será e9; em um ponto que x seja 12, a variação será e12 e assim por diante.
Além disso, se fôssemos calcular a área da curva a partir de um ponto, toda a área entre o eixo X e a curva, como representado na imagem, seria igual a ex . Então seguindo os pontos do exemplo que utilizamos anteriormente, no ponto x=9, a área seria e9 ; no ponto x=12, a área seria e12.
Isso traz inúmeras aplicações para cálculo, engenharia, física e praticamente tudo que envolva matemática.
Por fim, há também um logaritmo muito importante que utiliza o número de Euler, chamado de ln (ou logaritmo natural). Ele é a mesma coisa que o log de base “e”. Ou seja, a base desse logaritmo será aquela constante de 2,71828…
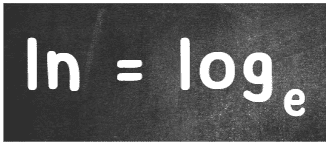
Em suma, o número de Euler irá aparecer em muitos lugares e, certamente, quando você estiver estudando sobre algoritmos de inteligência artificial e machine learning, você se deparará com ele.
Por isso, aprenda bem o conceito e volte nesse artigo sempre que quiser para relembrar alguma coisa. Se preferir, assista a videoaula abaixo, que contém este conteúdo:
Continue aprendendo
A matemática é essencial para um bom aprendizado das áreas de machine learning. Como você percebeu aqui, longe de ser um bicho de sete cabeças, é possível aprender conceitos matemáticos de forma clara e com exemplos didáticos.
Pensando nisso, desenvolvemos os cursos abaixo:
Ambos são grátis, curtos, e essenciais para aprofundar seus conhecimentos sobre análise de dados, machine learning e inteligência artificial.
Além disso, temos diversos outros cursos sobre esses assuntos. Todo nosso conteúdo é repleto de exemplos de fácil compreensão voltados para a o aprendizado do aluno. Clique aqui e confira.






























0 Comentários