A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?

A figura abaixo representa um avião que decolou sob um ângulo constante de 40º e percorreu em linha reta 8000 m. Nesta situação, qual a altura que se encontrava o avião ao percorrer essa distância?

Considere: sen 40º = 0,64; cos 40º = 0,77 e 

tg 40º = 0,84

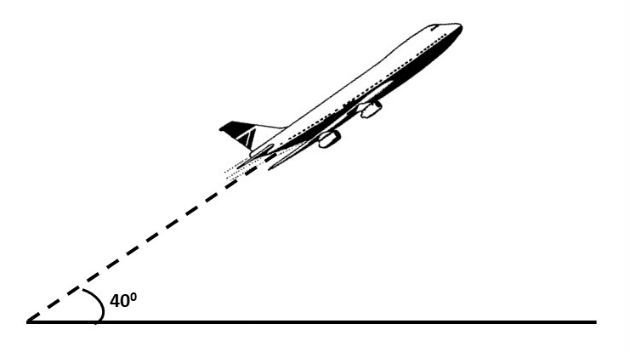
Resposta correta: 5 120 m de altura.

Vamos começar o exercício representando na figura a altura do avião. Para isso, basta desenhar uma reta perpendicular à superfície e que passa pelo ponto onde o avião se encontra.

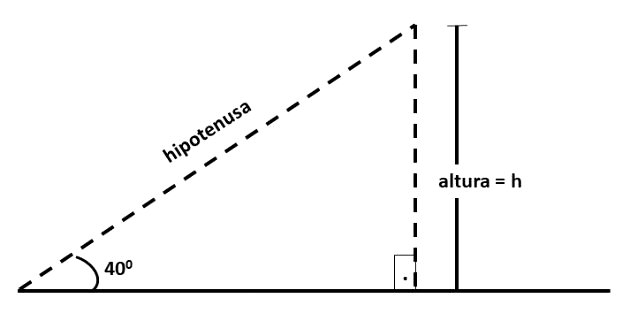
Notamos que o triângulo indicado é retângulo e a distância percorrida representa a medida da hipotenusa deste triângulo e a altura do cateto oposto ao ângulo dado.

Portanto, usaremos o seno do ângulo para encontrar a medida da altura:

Sen 40º - Cateto Oposto / Hipotenusa

Sen 40º = h/8000

Mas sen 40º = 0,64

Assim

0,64 = h/800

800*0,64 = 800*h/8000

h = 8000* 0,64

h = 5.120,00 m

Assim, ao percorrer 8 000 m, o avião se encontra a 5 120 m de altura.

Veja:

Lei dos senos

Um prédio projeta uma sombra de 40 m quando os raios solares (...)

Pagina 1 - Trigonometria

Pagina 2 - Trigonometria