Mundo Educação

Binômio de Newton

Conhecemos como binômio de Newton a técnica desenvolvida por Newton para calcular o polinômio que é resultado de uma potenciação de um binômio com um expoente natural.

Binômio de Newton é uma fórmula para calcular potências de um binômio.

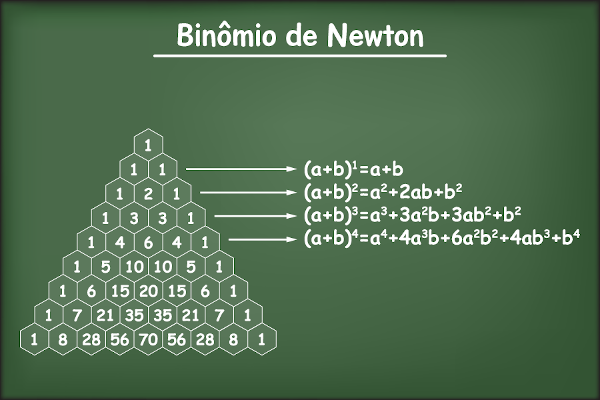
O binômio de Newton é um binômio qualquer elevado a um expoente natural. O nome é uma homenagem ao matemático Isaac Newton, que fez grandes contribuições para a Matemática, como o desenvolvimento de uma fórmula para calcular potências envolvendo binômios.

Newton percebeu que, ao resolver potências do tipo (a + b) n, existe uma regularidade, tornando possível o desenvolvimento de um método para encontrar o polinômio que é solução dessa operação. Além do desenvolvimento do binômio em si, é possível também encontrar o termo geral de um binômio.

Leia também: 4 dicas para aprender Matemática

Fórmula do binômio de Newton

Chamamos de binômio um polinômio que possui dois termos. Quando calculamos uma potência desse binômio, estamos calculando um binômio de Newton. O cálculo de uma potência de binômio é bastante comum em problemas da Física, Química e da própria Matemática, por isso é de grande importância compreender a fórmula desenvolvida por Newton.

Para entender a fórmula, calcularemos as potências de um binômio com expoentes menores. Quanto maior o expoente, mais difícil fica realizar esse cálculo.

(x+y)0 = 1

(x + y)1 = x + y

(x + y)2 = (x+y) (x+y) = x² + 2xy + y²

(x+y)³ = (x+y) (x+y)² = (x+y) (x² + 2xy + y²) = x³ + 3x²y + 3xy² +y³

É possível perceber que quanto maior for o expoente, maior será a solução do binômio de Newton e, por isso, torna-se conveniente utilizar a fórmula:

Exemplo:

Calcule (a + 2)4

Primeiro substituiremos na fórmula x = a, y = 2 e n = 4

Os coeficientes de cada termo são as combinações, conhecidas também como termos binomiais. Note que o expoente do primeiro termo, no caso a, começou em 4 no primeiro e foi decrescendo a cada termo. Já o expoente do segundo termo, no caso 2, começou em 0 e foi crescendo até chegar a 4.

Para calcular o coeficiente, utilizamos a fórmula da combinação:

Calculando as combinações, temos que:

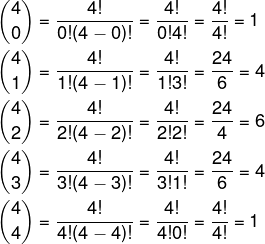
Substituindo na fórmula, encontramos o seguinte polinômio:

(a+2)4=1 · a4 + 4 · a3 · 2 + 6 · a2 · 22 + 4 · a · 23 + 1 · 24

Agora calcularemos as potências e as multiplicações:

(a+2)4=a4 + 8a3 + 6 · a2 · 4 + 4 · a · 8 + 1 · 16

(a+2)4=a4 + 8a3 + 24a2 + 32a + 16

Triângulo de Pascal

Uma propriedade importante do binômio de Newton é a sua relação com o triângulo de Pascal. Os coeficientes dos termos do binômio de Newton são iguais aos números encontrados nas linhas do triângulo.

Exemplo de triângulo de Pascal

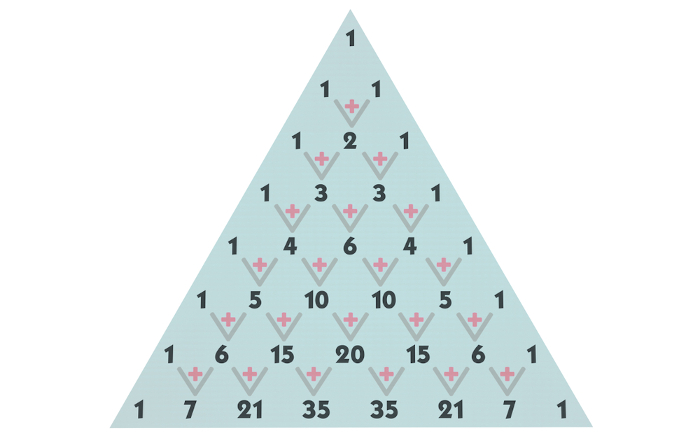
Com o triângulo de Pascal, torna-se desnecessário realizar o cálculo das combinações que acompanham cada um dos termos. Por exemplo, se o binômio for elevado a quatro, os coeficientes serão os números que aparecem na linha quatro do triângulo de Pascal.

É importante lembrar também que, no triângulo de Pascal, começamos a contar as linhas e as colunas a partir da linha 0 e da coluna 0. Utilizando o triângulo de Pascal, calcularemos o seguinte binômio de Newton:

Exemplo:

(a + b)6

Primeiro substituímos na fórmula:

Agora, em vez de calcular cada uma das combinações, basta olhar na linha 6 do triângulo de Pascal, que é composta pelos números 1, 6, 15, 20, 15, 6, 1. Então, substituiremos cada uma das combinações para esses valores, respeitando a ordem:

(a+b)6 = 1a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + 1b6

(a+b)6 = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6

Veja também: 3 conteúdos básicos de Matemática para o Enem

Termo geral do binômio de Newton

Algumas vezes, em vez de desenvolver todo o binômio de Newton, precisamos encontrar só um termo em específico. Para isso, existe a fórmula do termo geral do binômio de Newton.

p+1 → termo a ser encontrado

x → primeiro termo do binômio

y → segundo termo do binômio

n → expoente do binômio

Exemplo:

Dado o binômio (a+3)10, encontre o 4º termo do polinômio.

Como queremos o 4º termo, então:

p + 1 = 4

p = 4 – 1

p = 3

Além disso, temos que:

a → primeiro termo

3 → segundo termo

n→ 10

Então, substituindo na fórmula, temos que:

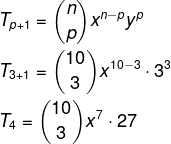
Calculando o binômio:

T4 = 120 · x7 · 27

T4 = 3.240

Leia também: Fórmulas de Matemática decisivas para o Enem

Exercícios resolvidos

Questão 1 - O coeficiente do termo a5 no resultado do binômio de Newton (a+2)8 é igual a:

A) 120

B) 224

C) 448

D) 560

E) 654

Resolução

Alternativa C.

Dados:

a → primeiro termo

2 → segundo termo

n → 8

Como queremos somente um termo em específico, utilizaremos a fórmula do termo geral, mas, antes, é necessário encontrar o valor de p.

Sabemos que:

an – p = a5

Logo, igualando os expoentes, temos que:

n – p = 5

Mas n = 8, então:

8 – p = 5

8 – 5 = p

3 = p

p = 3

Agora que conhecemos todos os valores necessários, substituiremos na fórmula:

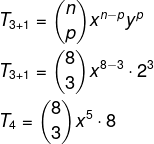
Vamos calcular a combinação:

Por fim:

T4 = 56 · x5 · 8

T4 = 448

Questão 2 - A soma dos coeficientes do polinômio encontrado ao calcular a potência (a + b)5 é:

A) 12

B) 24

C) 64

D)16

E) 32

Resolução

Alternativa E.

Sabemos que, nesse caso, como os dois termos são algébricos, os coeficientes são apenas os números encontrados na quinta linha do triângulo de Pascal.

linha 0: 1

linha 1: 1 1

linha 2: 1 2 1

linha 3: 1 3 3 1

linha 4: 1 4 6 4 1

linha 5: 1 5 10 10 5 1

A soma dos termos da linha 5 é:

1 + 5 + 10 + 10 + 5 + 1 = 32