Ângulo Central e Ângulo Inscrito – Dedução da relação
Clubes OBMEP - Dedução da relação
Ângulos na circunferência e polígonos inscritos
Ângulos na circunferência:
Ângulo central: seu vértice está no centro da circunferência (Ângulo central relativo a um círculo é o ângulo que tem o vértice no centro do círculo. Ângulo inscrito relativo a um círculo é um ângulo que tem o vértice no círculo e os lados são secantes a ele.).
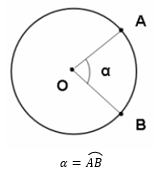
Ângulo inscrito: seu vértice é um ponto da circunferência ( é um ângulo que tem o vértice no círculo e os lados são secantes a ele. Um ângulo inscrito é metade do ângulo central correspondente; ou pode-se dizer: a medida de um ângulo inscrito é metade da medida do arco correspondente).
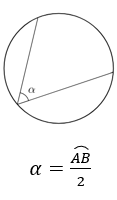
Ângulo de segmento: formado por uma corda e uma tangente (com vértice no ponto de tangência - O ângulo é conhecido como ângulo de segmento quando ele é formato por um segmento de reta tangente à circunferência e o outro não. Quando isso ocorre, o ângulo é igual à metade do arco.).
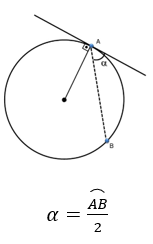
Ângulo excêntrico interno: formado por duas cordas (um ângulo é conhecido como excêntrico interno quando ele não está no centro da circunferência, mas está localizado na parte interior da circunferência, não podendo ser um ângulo inscrito. Quando isso ocorre, podemos definir dois arcos. O ângulo será a média aritmética entre eles, ou seja, a soma dividida por dois).
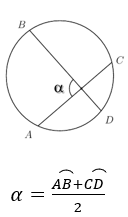
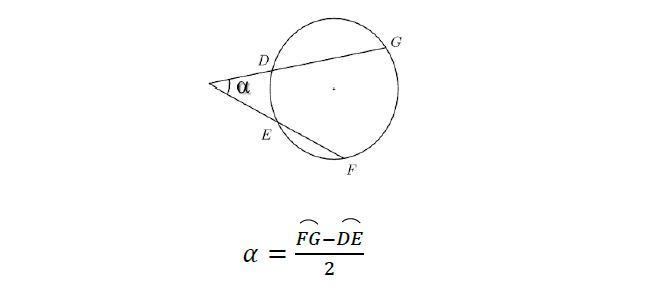
Ângulo excêntrico externo: formado por duas retas secantes à circunferência (conhecemos como excêntrico externo o ângulo que é externo à circunferência. Quando isso ocorre, ele forma dois arcos, e o valor do ângulo é calculado pela metade da diferença entre o arco maior e o arco menor).
Polígonos inscritíveis
Quadrilátero
Um quadrilátero é inscritível se, e somente se, seus ângulos opostos são suplementares.
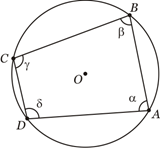
α + y = β + δ
Triângulo retângulo
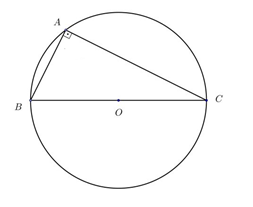
Se um triângulo retângulo é inscrito em meia circunferência, então sua hipotenusa coincide com o diâmetro da circunferência.






























0 Comentários