Pontos notáveis de um triângulo: quais são e como localizar
No estudo dos triângulos, o baricentro, o ortocentro, o incentro e o circuncentro são pontos de grande importância, isto porque, cada um deles traz propriedades e características que auxiliam a resolução de diversos problemas.
Estes pontos, conhecidos por pontos notáveis, são determinados pelo cruzamento de um conjunto de linhas, conhecidas como cevianas. Como um triângulo possui três lados e três vértices, todo triângulo possui três de cada uma destas linhas.
Baricentro
O baricentro é o ponto de encontro (interseção) entre as três medianas (A Mediana pode representar diversos fenômenos, porém dentro do contexto geométrico, ela é o segmento de reta que liga um vértice de um triângulo à metade (ponto médio) da aresta oposta a este ponto) de um triângulo. Lembre-se que mediana é o segmento que vai de um vértice até o meio do lado oposto.
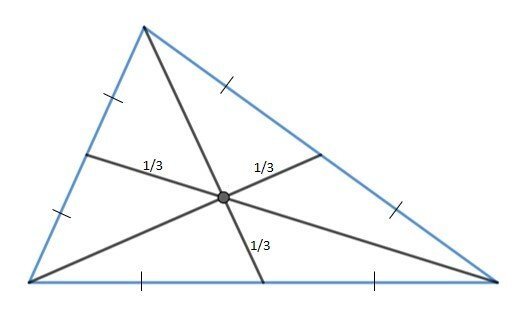
Uma propriedade do baricentro é que ele divide a mediana em duas partes, onde a menor, equivale a 1/3 da própria mediana.
Outra propriedade interessante do baricentro é que ele determina o centro de massa, ou de gravidade, do triângulo.
Ortocentro
O ortocentro é o ponto de encontro (interseção) entre as três alturas (A altura de um triângulo é o segmento que liga um ponto a seu segmento oposto (base oposta), formando com ele um ângulo de 90°. Dizemos que a altura de um triângulo é sempre perpendicular à sua base) de um triângulo. Lembre-se que altura é o segmento que vai de um vértice até o lado oposto, fazendo 90°.
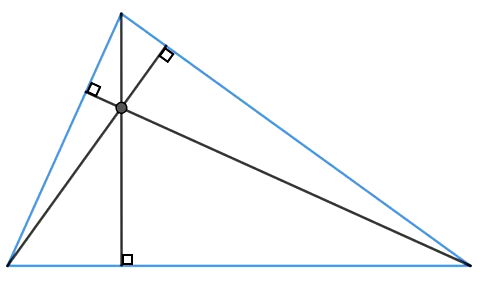
O ortocentro também pode estar sobre o triângulo, caso seja retângulo, ou fora, se for obtusângulo.
Incentro
O incentro é o ponto de encontro (interseção) entre as três bissetrizes ("Bissetriz é a semirreta interna de um ângulo traçada a partir do vértice deste, dividindo-o em dois ângulos congruentes. As bissetrizes de um triângulo se encontram em um ponto conhecido como incentro, que é o centro da circunferência inscrita nesse polígono"
Veja mais sobre "Bissetriz" em: https://brasilescola.uol.com.br/matematica/bissetriz.htm) de um triângulo. Uma bissetriz é um segmento que divide um ângulo ao meio, ou seja, determina dois iguais.
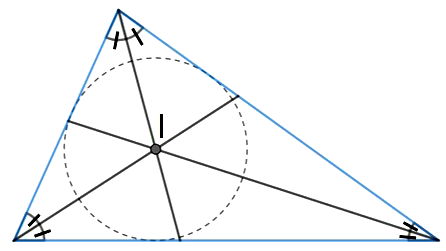
O incentro também é o centro da circunferência inscrita (que está dentro) no triângulo. Na imagem acima, é a circunferência pontilhada.
A distância entre o incentro e os lados do triângulo é a mesma para os três lados. Esta distância é exatamente o raio desta circunferência.
O incentro sempre está no interior do triângulo, independente da forma do triângulo, uma vez que é o centro da circunferência inscrita.
Circuncentro
É o ponto de encontro (interseção) entre as três mediatrizes. Uma mediatriz é uma reta que corta um segmento no seu ponto médio, com um ângulo de 90°.
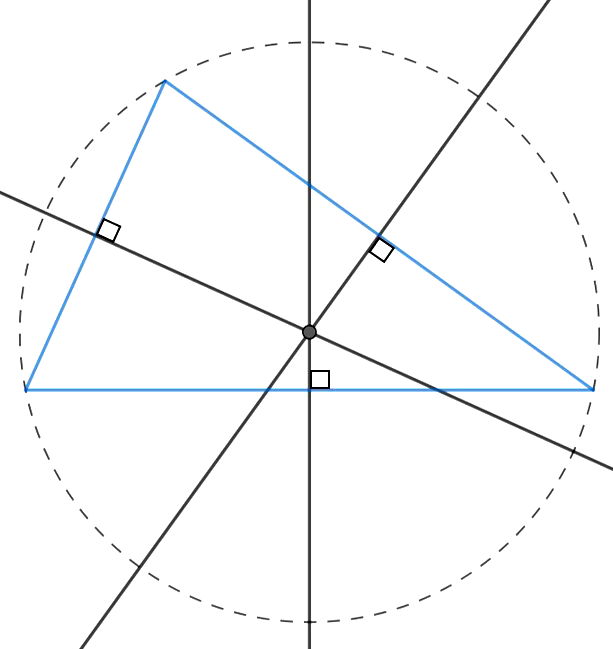
O circuncentro é o centro da circunferência circunscrita ao triângulo. Os três vértices do triângulo pertencem a esta circunferência. Por isto, os vértices estão a mesma distância do circuncentro e, esta distância, é o próprio raio da circunferência.
É importante notar que o circuncentro pode estar fora do triângulo, ou mesmo sobre o triângulo. No exemplo acima o triângulo é acutângulo (três ângulos menores que 90°) e o circuncentro está no triângulo.
Se o triângulo for retângulo, o circuncentro estará sobre um lado do triângulo.
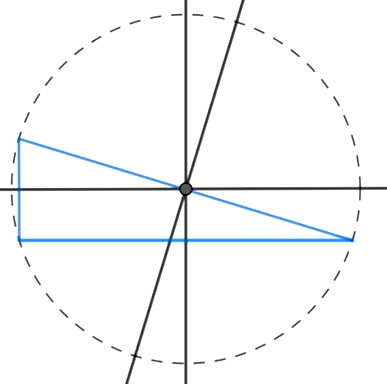
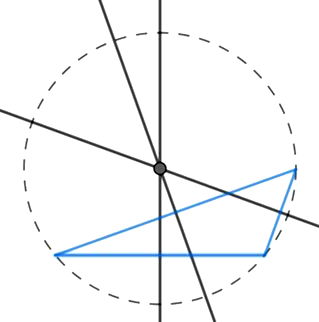
Se o triângulo for obtusângulo, o circuncentro estará fora do triângulo.
Pontos notáveis e cevianas
Como cada ponto notável de um triângulo é formado pelo cruzamento entre as cevianas, esta tabela ajuda distinguir cada uma.
| Ponto notável | ceviana |
|---|---|
| baricentro | medianas |
| ortocentro | alturas |
| incentro | bissetrizes |
| circuncentro | mediatrizes |
Altura, mediana, bissetriz e mediatriz em um triângulo
Estes segmentos são importantes no estudo da geometria e dos triângulos. Identifique no triângulo da imagem a seguir, estes quatro segmentos.
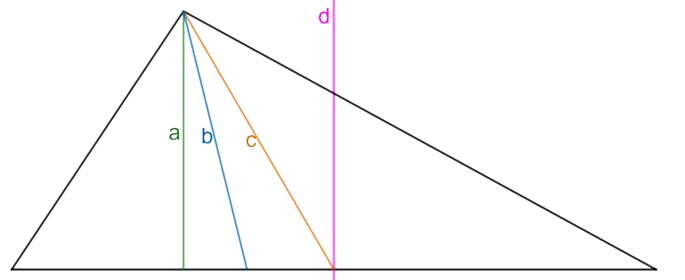
a é a altura;
b é a bissetriz;
c é mediana;
d é a mediatriz.









































0 Comentários