Bissetriz
Conhecemos como bissetriz a semirreta interna de um ângulo traçada a partir de seu vértice, dividindo-o em dois ângulos congruentes.
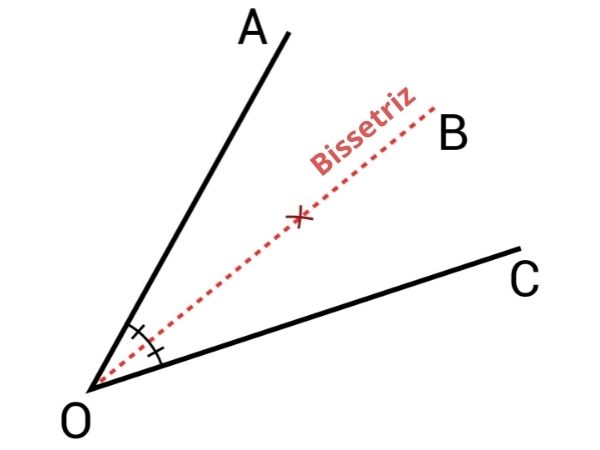
Bissetriz é a semirreta interna de um ângulo traçada a partir do vértice deste, dividindo-o em dois ângulos congruentes. As bissetrizes de um triângulo se encontram em um ponto conhecido como incentro, que é o centro da circunferência inscrita nesse polígono.
A partir da bissetriz foram elaborados dois teoremas importantes: o do ângulo interno e o do ângulo externo, desenvolvidos em triângulos que utilizam a proporção para relacionar os lados desse polígono. No plano cartesiano, é possível traçar a bissetriz nos quadrantes ímpares e nos pares.
Leia também: Pontos notáveis de um triângulo
Tópicos deste artigo
- 1 - Resumo sobre bissetriz
- 2 - O que é bissetriz?
- 3 - Como encontrar a bissetriz?
- 4 - Bissetriz de um triângulo
- 5 - Teorema da bissetriz interna
- 6 - Teorema da bissetriz externa
- 7 - Bissetriz dos quadrantes do plano cartesiano
- 8 - Exercícios resolvidos sobre bissetriz
Resumo sobre bissetriz
A bissetriz é uma semirreta que divide um ângulo em dois ângulos congruentes.
Podemos traçar as bissetrizes de ângulos internos de triângulos.
A partir da bissetriz de um ângulo do triângulo foi desenvolvido o teorema do ângulo interno.
Existem duas bissetrizes no plano cartesiano, a dos quadrantes pares e a dos quadrantes ímpares.
O que é bissetriz?
Dado um ângulo AOB, chamamos de bissetriz a semirreta OC, que parte do ponto O e divide o ângulo AOB em dois ângulos congruentes.
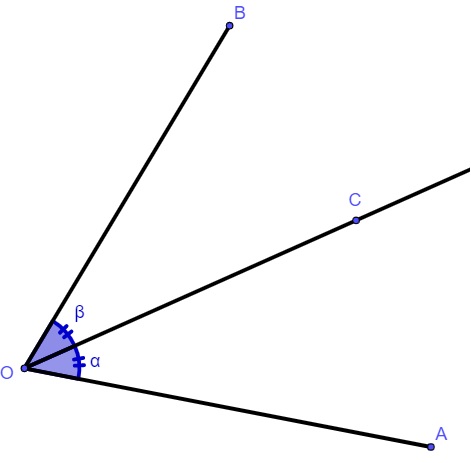
Na imagem, a semirreta OC é a bissetriz do ângulo AOB.
Como encontrar a bissetriz?
Para encontrar a bissetriz, são utilizados como instrumentos uma régua e um compasso e são seguidos os passos a seguir:
1º passo: Coloca-se a ponta seca do compasso sob o vértice O e é feito um arco sobre as semirretas OA e OB.
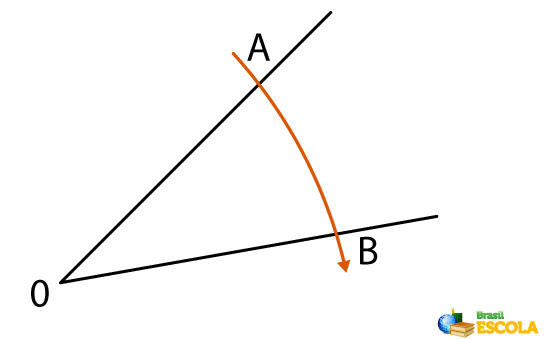
2º passo: Coloca-se a ponta seca do compasso no ponto de intersecção do arco com a semirreta OA e é feito um arco com o compasso virado para a parte interna do ângulo.
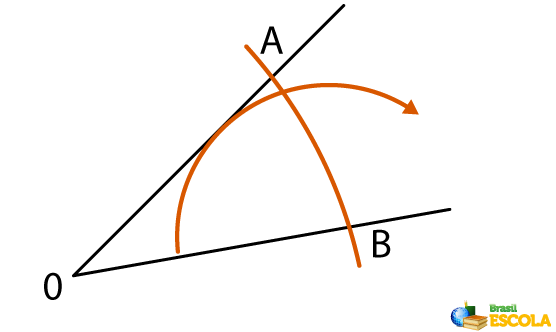
3º passo: No ponto de intersecção do arco com a semirreta OB coloca-se a ponta seca do compasso e repete-se o processo anterior.
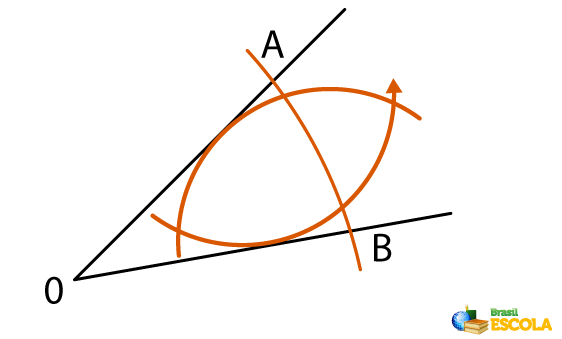
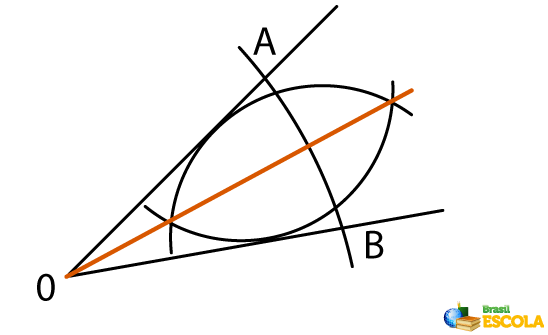
4º passo: Por fim, ao traçar uma semirreta do vértice do ângulo que passa pelos pontos de intersecção entre os arcos, a bissetriz do ângulo é encontrada.
Leia também: Baricentro — um dos pontos notáveis de um triângulo
Bissetriz de um triângulo
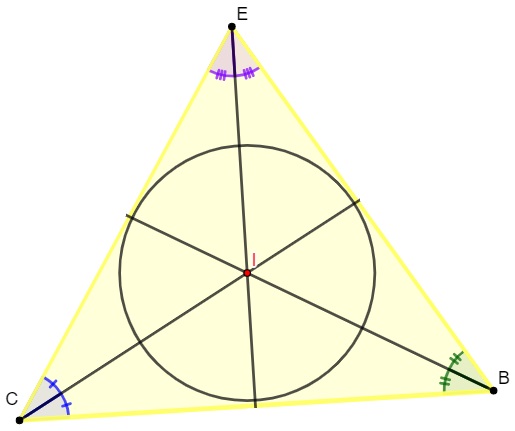
Quando são traçadas as bissetrizes dos ângulos internos de um triângulo, podemos encontrar seu ponto notável, conhecido como incentro, que é o ponto de encontro das bissetrizes e também o centro da circunferência inscrita no polígono.
Teorema da bissetriz interna
São formados segmentos proporcionais aos lados adjacentes de um triângulo quando traçamos a bissetriz de um de seus ângulos internos.
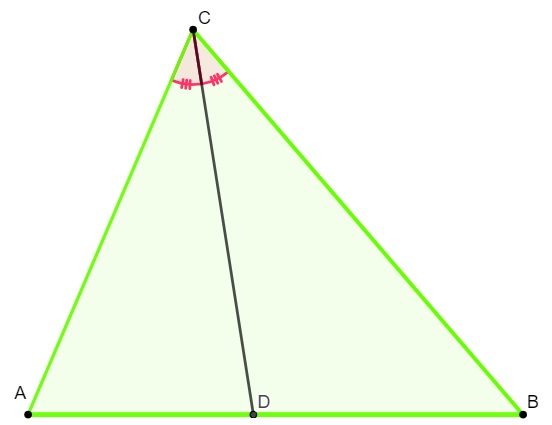
![]()
Exemplo:
Dado o triângulo a seguir, encontre o comprimento do lado AC.
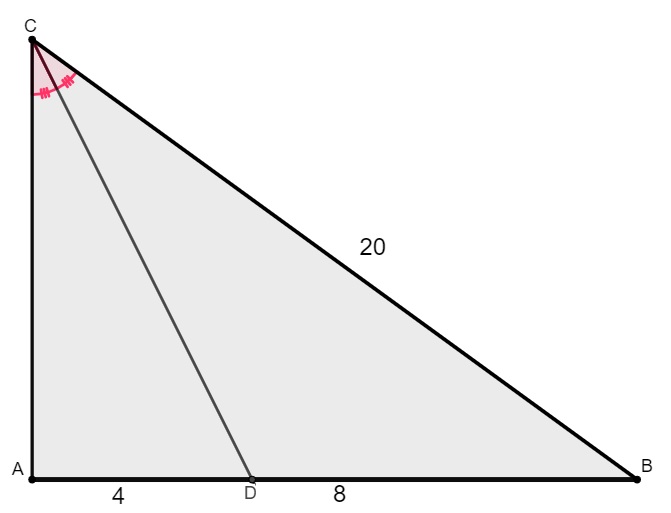
Resolução:
Aplicando o teorema da bissetriz interna, calcula-se:
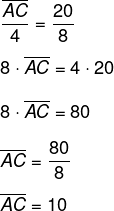
Videoaula sobre teorema da bissetriz interna
Teorema da bissetriz externa
Quando a bissetriz de um dos ângulos externos de um triângulo é traçada, o prolongamento do lado oposto ao ângulo externo forma segmentos proporcionais aos lados adjacentes.
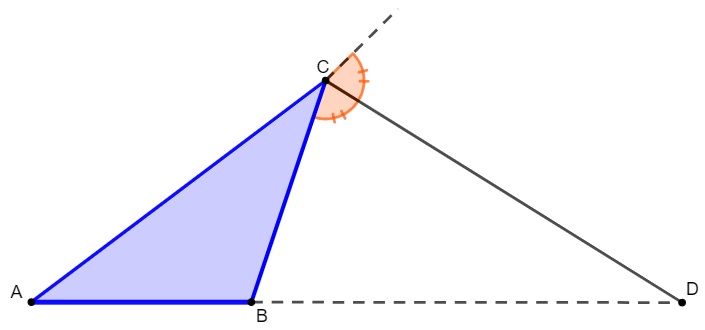
![]()
Exemplo:
Encontre o valor de x.
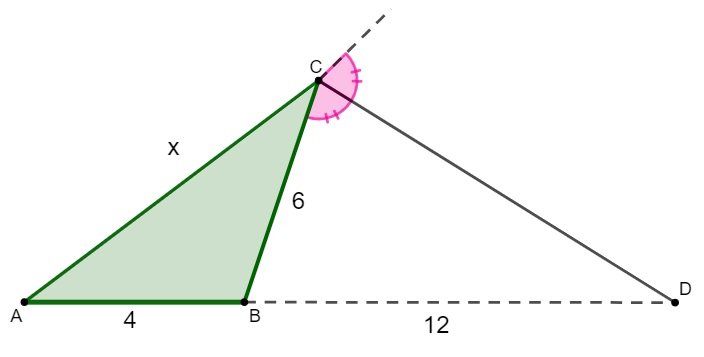
Aplicando o teorema da bissetriz externa, temos que:
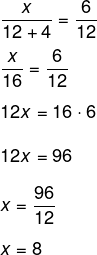
Bissetriz dos quadrantes do plano cartesiano
É possível traçar a bissetriz no plano cartesiano. Existem duas possibilidades: a bissetriz que passa pelos quadrantes pares e a que passa pelos quadrantes ímpares.
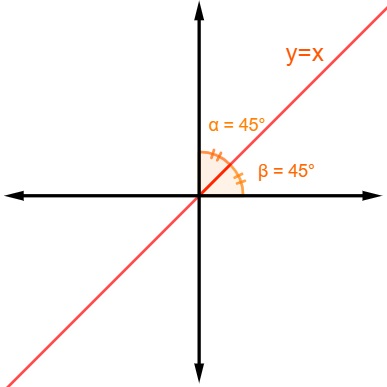
A bissetriz dos quadrantes ímpares passa pelos 1º e 3º quadrantes. Quando a bissetriz corta os quadrantes ímpares, a sua equação é y = x. Logo, os pontos pertencentes à bissetriz dos quadrantes pares possuem abcissa e ordenada iguais.
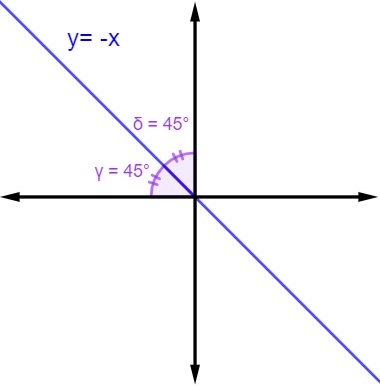
O segundo caso se refere a quando a bissetriz passa pelos quadrantes pares, ou seja, pelos 2º e 4º quadrantes. Quando isso ocorre, a equação da reta será y = – x. Logo, os pontos possuem abcissa e ordenada como números simétricos.
Leia também: Teorema fundamental da semelhança — a relação entre uma reta paralela e o lado de um triângulo
Exercícios resolvidos sobre bissetriz
Questão 1
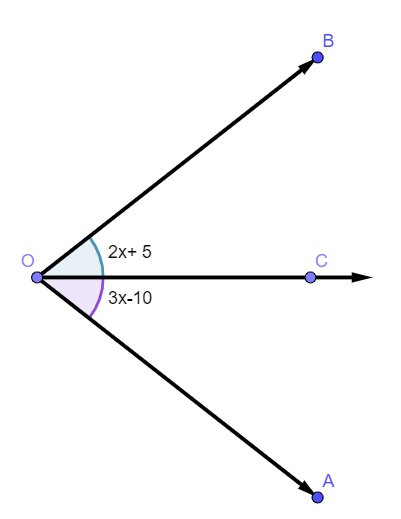
Na imagem a seguir, sabendo que OC é a bissetriz do ângulo AOB, podemos afirmar que a medida do ângulo AOB é igual a
A) 15°
B) 30°
C) 35°
D) 60°
E) 70º
Resolução:
Alternativa E
Como OC é bissetriz, temos o seguinte:
3x – 10 = 2x + 5
3x – 2x = 10 + 5
x = 15°
Sabe-se que x = 15 e que o valor da metade do ângulo AOB é igual a 2x + 5. Substituindo x por 15, obtém-se:
2 · 15 + 5
30 + 5
35°
A metade do ângulo AOB é de 35°. Logo, o ângulo AOB é igual ao dobro de 35°, ou seja,
AOC = 35 · 2 = 70°.
Questão 2
Em um triângulo foram traçadas as suas três bissetrizes internas. Após traçá-las, foi possível perceber que elas se encontram em um ponto. O ponto de encontro das bissetrizes de um triângulo é conhecido como
A) baricentro.
B) incentro.
C) circuncentro.
D) ortocentro.
Resolução:
Alternativa B
Quando as bissetrizes internas de um triângulo são traçadas, o ponto de encontro delas é conhecido como incentro.
Por Raul Rodrigues de Oliveira
Professor de Matemática
OLIVEIRA, Raul Rodrigues de. "Bissetriz"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/bissetriz.htm. Acesso em 30 de maio de 2023.












.jpeg)


























0 Comentários