Número Pi

Rafael Asth

Professor de Matemática e Física

O volume da esfera é calculado em função do seu raio onde, o raio, corresponde à distância entre o centro e qualquer ponto da superfície.

A esfera é um sólido geométrico espacial, formado por todos os pontos do espaço que estão a uma distância do centro, igual ou menor que o raio.

Número Pi (π) é um número irracional cujo valor é 3,14159265358979323846…, ou seja, uma sequência infinita de dígitos.

Como Calcular?

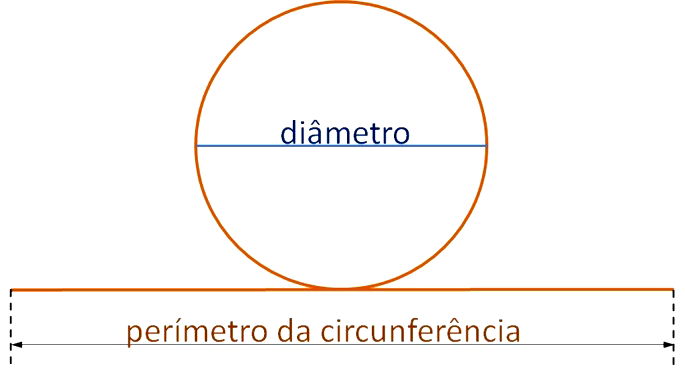
O Pi resulta da divisão do perímetro pelo diâmetro de um círculo.

Se medirmos toda a volta de um círculo com fita métrica obtemos a medida do seu perímetro. O diâmetro, por sua vez, é a medida obtida de uma extremidade a outra desse círculo, passando pelo centro.

Dividindo a medida do perímetro pela medida do diâmetro, o resultado será o número pi.

História

Estudado desde a antiguidade, conforme mostram os registros históricos, o número pi continua aguçando a curiosidade dos estudiosos. O motivo é que o seu cálculo resulta em trilhões de casas decimais.

Entre os babilônios e os egípcios foram encontrados cálculos que se aproximavam do Pi. Eles já sabiam que a razão entre o perímetro e o diâmetro era superior a 3.

Mas foi apenas no século XVIII que o mesmo passou a fazer parte dos símbolos matemáticos. O primeiro a propor a sua utilização foi o matemático galês William Jones.

O símbolo (π) é uma letra grega minúscula, a primeira da palavra περίμετρος, que significa “perímetro” (em português).

É denominado de Constante de Arquimedes. Isso porque foi o matemático Arquimedes a primeira pessoa a calcular e obter a razão entre o perímetro e o diâmetro.

Mas depois de Arquimedes, o cientista Ptolomeu conseguiu se aproximar ainda mais do valor de Pi.

O número Pi é infinito. Por esse motivo, ele é representado com reticências no fim. No entanto, muitas vezes utiliza-se apenas a aproximação para 3,1416, ou 3,14, para facilitar os cálculos matemáticos.

Importa referir que as calculadoras limitam o números de casas decimais, pois não cabem tantas casas nelas. A descoberta de tantas casas tornou-se possível graças aos computadores.

Saiba mais sobre os números irracionais e os demais conjuntos numéricos.

Para que serve?

Vejamos um exemplo.

Calcule a área da lateral de um cilindro cujo raio tem 6 cm e a medida da altura é duas vezes o raio.

Considere pi igual a 3,14.

A fórmula para calcular a área lateral do cilindro é:

Al = 2π * r * h

Onde,

Al: área lateral

π: Pi
r: raio

h: altura

Saiba mais:

Como Newton e Leibniz chegaram ao número Pi?

Isaac Newton e Gottfried Wilhelm Leibniz, independentemente um do outro, desenvolveram métodos inovadores para calcular o valor de Pi (π) no final do século XVII.

Método de Newton:

Séries infinitas: Newton utilizou séries infinitas, como a série de Madhava-Leibniz, para aproximar o valor de Pi.
Polinômios: Ele também utilizou polinômios para calcular o valor de Pi com maior precisão.
Cálculo infinitesimal: O cálculo infinitesimal, inventado por Newton, foi fundamental para seus métodos.

Método de Leibniz:

Séries infinitas: Leibniz também utilizou séries infinitas, como a série de Madhava-Leibniz, para aproximar o valor de Pi.
Soma de áreas: Ele utilizou o método de soma de áreas de retângulos inscritos em um círculo para calcular o valor de Pi.
Cálculo infinitesimal: O cálculo infinitesimal, inventado por Leibniz, também foi fundamental para seus métodos.

Comparação dos métodos:

Similaridades: Ambos os métodos utilizaram séries infinitas e o cálculo infinitesimal.
Diferenças: Newton utilizou polinômios, enquanto Leibniz utilizou a soma de áreas.
Precisão: O método de Leibniz era mais preciso que o de Newton na época.

Contribuições:

Newton e Leibniz: Foram pioneiros no uso de métodos matemáticos rigorosos para calcular o valor de Pi.
Século XVII: A partir de seus trabalhos, o cálculo de Pi tornou-se mais preciso e eficiente.
Atualidade: Os métodos de Newton e Leibniz ainda são utilizados para calcular o valor de Pi.

Observações:

Cálculo infinitesimal: Essa ferramenta matemática foi fundamental para o avanço do cálculo de Pi.
Precisão: A busca por um valor cada vez mais preciso de Pi continua até hoje.
Aplicações: O número Pi tem diversas aplicações em matemática, física, engenharia e outras áreas.

Para aprofundar seus conhecimentos: