Considere um prisma triangular com bases na forma de triângulos equiláteros com lados de 6 cm. Se sua altura também possui 6 cm, determine seu volume e área superficial total.

Resposta: o volume é de 93,6 m³ e a área é de 139,2 cm², aproximadamente.

Cálculo do volume.

O volume de todo prisma é calculado pelo produto entre a área da base e a altura.

V = A * h

$reto V espaço igual a espaço reto A com reto b subscrito espaço. espaço reto h$

Sendo a base um triângulo equilátero, sua área pode ser calculada por:

A = b*h/2

$reto A com reto b subscrito igual a numerador reto b espaço. espaço reto h sobre denominador 2 fim da fração$

Para determinar a altura do triângulo da base, utilizamos o teorema de Pitágoras no triângulo retângulo:

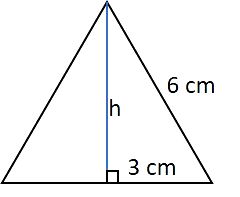
6² = 3² + h²

36 = 9 + h²

36 - 9 = 9 + h² - 9

27 = h²

h = sqrt(27)

h = 3 * sqrt(3)

$6 ao quadrado igual a 3 ao quadrado espaço mais espaço reto h ao quadrado 36 espaço igual a espaço 9 espaço mais espaço reto h ao quadrado 36 espaço menos espaço 9 espaço igual a espaço reto h ao quadrado 27 espaço igual a espaço reto h ao quadrado raiz quadrada de 27 espaço igual a espaço reto h$

A área da base é:

$reto A com reto b subscrito igual a numerador 6 espaço. espaço raiz quadrada de 27 sobre denominador 2 fim da fração igual a 3 raiz quadrada de 27 espaço c reto m$

O volume é:

V = A * h

V = 3 sqrt(27) * 6

V = 18 * sqrt (27)

$V espaço igual a espaço A com b subscrito espaço. espaço h V espaço igual a espaço 3 raiz quadrada de 27 espaço. espaço 6 V espaço igual a espaço 18 raiz quadrada de 27 espaço c m ao cubo$

Aproximando a raíz de 27 para 5,2:

v = 18 * 5,2 = 93,6 cm³

$reto V igual a 18 espaço. espaço 5 vírgula 2 espaço igual a espaço 93 vírgula 6 espaço cm ao cubo$

Cálculo da área superficial total.

O prisma triangular é formado por duas bases triangulares e três retângulos. Como já calculamos a área da base, basta multiplicar por dois.

Área das bases.

2 * 3 sqrt(27) cm²=

6 sqrt(27) cm²=

18 sqrt(3) cm²

$2 espaço. espaço 3 raiz quadrada de 27 igual a 6 raiz quadrada de 27 espaço c m ao quadrado$

Área lateral.

São três quadrados formados por 6 cm de lado.