Análise Combinatória | (RFB – ESAF 2009). Sabe-se que os pontos A,B,C, D, E, F e G são coplanares, ou seja, estão localizados no mesmo plano ...

https://sabermatematica.com.br/analisecombinatoriaer.html

Questão 6 (RFB – ESAF 2009). Sabe-se que os pontos A,B,C, D, E, F e G são coplanares, ou seja, estão localizados no mesmo plano. Sabe-se, também, que destes sete pontos, quatro são colineares, ou seja, estão numa mesma reta. Assim, o número de retas que ﬁcam determinadas por estes sete pontos é igual a:

a) 16

b) 28

c) 15

d) 24

e) 32

Resolução

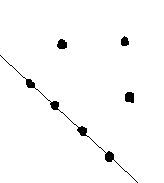
Vejamos na figura abaixo como estão dispostos os pontos:

A questão pode ser resolvida de duas formas distintas:

Resolução 1

Temos que dois pontos bastam para determinar uma reta, então basta fazer a combinação dos 7 pontos tomados 2 a 2, subtraindo a combinação dos 4 pontos (colineares) tomados 2 a 2, somando a reta que passa pelos 4 pontos colineares.

C7,2 – C4,2 + 1 = 7!/(7-2)!2! – 4!/(4-2)!2! + 1 = 21 – 6 + 1 = 16

Resolução 2

Cada um dos 3 pontos não colineares pode ser ligado nos 4 pontos colineares, ou seja, cada um forma 4 retas, daí, temos 3 x 4 = 12 retas.

Podemos também formar 3 retas utilizando apenas os 3 pontos não colineares.

Por último, uma reta que passa pelos 4 pontos colineares.

Logo, 12 + 3 + 1 = 16

Resposta: A

Jordon: Graduado e mestre em matemática pela Universidade Federal do Espírito Santo. Trabalha no BB há 15 anos e atua como professor de matemática nas horas vagas.

Links:

Análise Combinatória - Página 1

Análise Combinatória - Página 2

Análise Combinatória - Página 3

Análise Combinatória - Página 4

Análise Combinatória - Página 14

Análise Combinatória - Página 17

Análise Combinatória - Página 19