Trigonometria || Um menino avista o ponto mais alto de um morro, conforme figura abaixo. Considerando que ele está a uma distância de 500 m da base do morro, calcule a altura (h) deste ponto.

 

Um menino avista o ponto mais alto de um morro, conforme figura abaixo. Considerando que ele está a uma distância de 500 m da base do morro, calcule a altura (h) deste ponto.

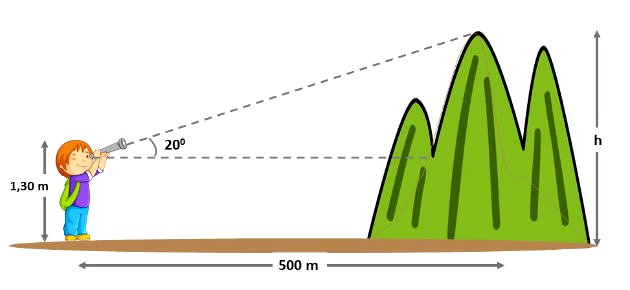
Considere:

sen 20º = 0,34

cos 20º = 0,93

tg 20º = 0,36

Resposta correta: 181,3 m.

Observando o desenho, notamos que o ângulo visual é de 20º. Para calcular a altura do morro, iremos usar as relações do seguinte triângulo:

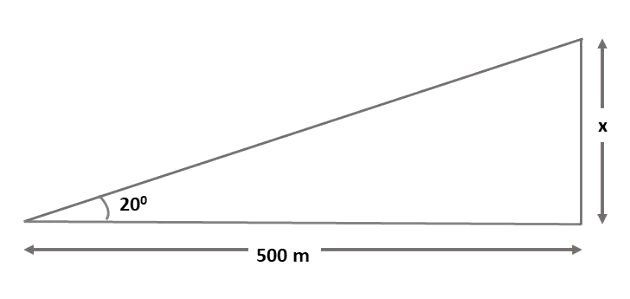
Como o triângulo é retângulo, iremos calcular a medida x usando a razão trigonométrica tangente.

Escolhemos essa razão, visto que conhecemos o valor do ângulo do cateto adjacente e estamos procurando a medida do cateto oposto (x).

Assim, teremos:

Tg 20º = x / 500 m

0,36 = x / 500 m

0,36 * 500 m = x

x = 180 m

Como o menino tem 1,30 m, a altura do morro será encontrada somando-se este valor ao valor encontrado para x. Assim, teremos:

======================

h = 180 m + 1,30 m =181,3o m

======================

Logo, a altura do morro será igual a 181,3 m.