Trigonometria || Pedro, localizado a 8 metros do chão, está observando o prédio vizinho. Sabendo que a sua distância para o prédio vizinho é de 8 m e entre as duas estruturas forma-se um triângulo, cujo ângulo ABC é de 105º, determine a altura do prédio que Pedro está observando.

 

Pedro, localizado a 8 metros do chão, está observando o prédio vizinho. Sabendo que a sua distância para o prédio vizinho é de 8 m e entre as duas estruturas forma-se um triângulo, cujo ângulo ABC é de 105º, determine a altura do prédio que Pedro está observando.

Ver Resposta

Resposta correta: 21,86 m.

No desenho, ao efetuarmos a projeção do ponto B no prédio que Pedro está observando, dando a ele o nome de D, criamos o triângulo isósceles DBC.

O triângulo isósceles possui dois lados iguais e, portanto, DB = DC = 8 m.

Os ângulos DCB e DBC possuem o mesmo valor, que é 45º. Observando o triângulo maior, formado pelos vértices ABD encontramos o ângulo de 60º, pois subtraímos o ângulo de ABC pelo ângulo de DBC.

ABD = 105º - 45º = 60º.

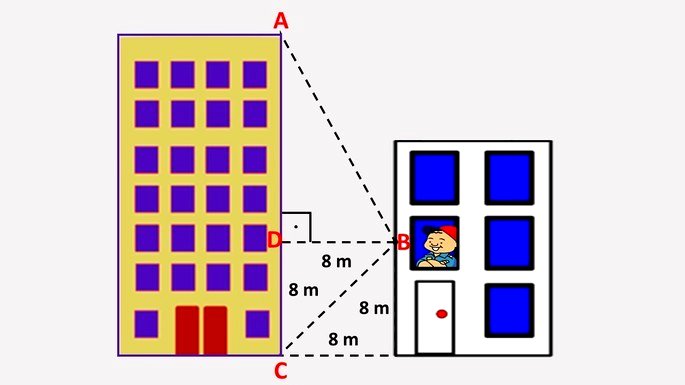
Sendo assim, o ângulo DAB é de 30º, já que a soma dos ângulos internos deve ser 180º.

DAB = 180º - 90º - 60º = 30º.

Utilizando a função tangente, Tg = Cateto Oposto/Cateto adjacente , encontramos a medida do lado AD, que corresponde ao cateto adjacente do triângulo ABD. O cateto oposto possui o valor de 8m.

Tg = Cateto Oposto/Cateto adjacente 

Tg 30º = 8/Cateto Adjacente

Cateto Oposto = 8/Tg 30º = 8/0,577 = 13,86 m

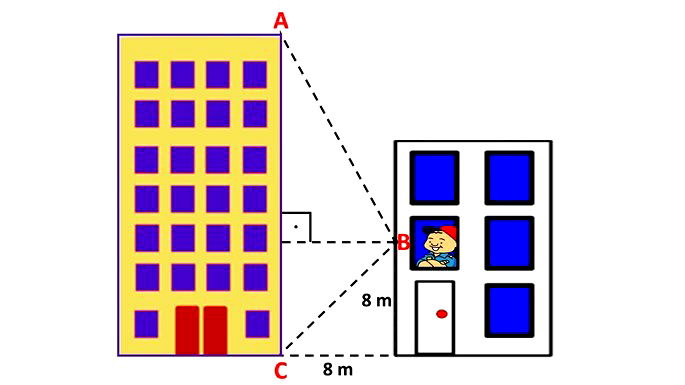
A altura do prédio representa a distância entre os vértices A e C, sendo assim:

AC = = 13,86 m + 8 m

AC = 21,86 m

Portanto, a altura do prédio é de 21,86 m.