Trigonometria || (Epcar - 2016) As cidades A, B e C situam-se às margens de um rio e são abastecidas por uma bomba situada em P, conforme figura abaixo.

 

(Epcar - 2016) As cidades A, B e C situam-se às margens de um rio e são abastecidas por uma bomba situada em P, conforme figura abaixo.

Sabe-se que o triângulo ABC é retângulo em B e a bissetriz do ângulo reto corta AC no ponto P. Se BC = 6√3 km, então CP é, em km, igual a

a) 6 +√3

b) 6(3 − √3 )

c) 9 √3 − √2

d) 9(√ 2 − 1)

Alternativa correta: b) 6(3 − √3 ).

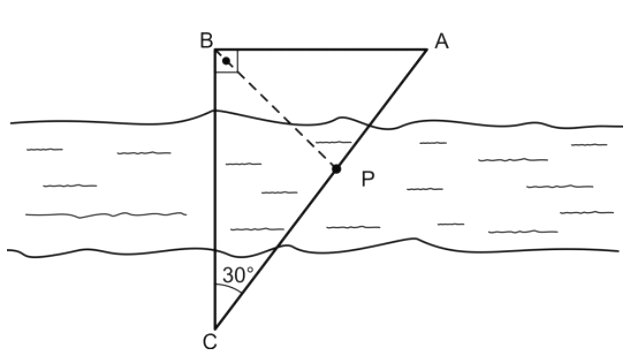
Podemos começar calculando o lado BA através das razões trigonométricas, visto que o triângulo ABC é retângulo e temos a medida do ângulo formado pelos lados BC e AC.

O lado BA é oposto ao ângulo dado (30º) e o lado BC é adjacente a este ângulo, portanto, iremos calcular usando a tangente de 30º:

TG 30º = BA/BC

SQRT (3)/3 = BA/[6 SQRT (3)]

BA = 6 SQRT (9)/3

BA = 6

Usando o Teorema de Pitágoras, podemos encontrar a medida do lado AC, que é a hipotenusa do triângulo retângulo:

AC² = BA² + BC²

AC² = 6 ² + [6 SQRT (3)]²

AC² = 144

AC = 12

Agora que já conhecemos as medidas dos lados do triângulo ABC, podemos calcular a medida do lado CP através do teorema da bissetriz interna.

Para isso, observe que o lado PA é igual a 12 - PC, aplicando o teorema da bissetriz interna, temos:

PB/PC = BA/PA

6 SQRT (3) / PC = 6 / (12 - PC)

6 PC = 72 SQRT (3) - 6 SQRT (3) PC

PC = 6 ( 3 - SQRT (3))

Alternativa b: 6(3 − √3 )