Potenciação
A potenciação ou exponenciação é a operação matemática que representa a multiplicação de fatores iguais. Ou seja, usamos a potenciação quando um número é multiplicado por ele mesmo várias vezes.
Para escrever um número na forma de potenciação usamos a seguinte notação:
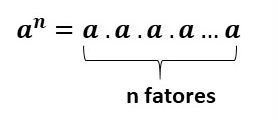
Sendo a ≠ 0, temos:
Para melhor entender a potenciação, no caso do número 23 (dois elevado a terceira potência ou dois elevado ao cubo), tem-se:
23 = 2 x 2 x 2 = 4 x 2 = 8
Sendo,
Exemplos de Potenciação
52: lê-se 5 elevado à segunda potência ou 5 ao quadrado, donde:
5 x 5 = 25
Logo,
A expressão 52 equivale a 25.
33: lê-se 3 elevado à terceira potência ou 3 ao cubo, donde:
3 x 3 x 3 = 27
Logo,
A expressão 33 equivale a 27.
Propriedades da Potenciação
- Toda potência com expoente igual a zero, o resultado será 1, por exemplo: 50=1
- Toda potência com expoente igual 1, o resultado será a própria base, por exemplo: 81 = 8
- Quando a base for negativa e o expoente um número ímpar, o resultado será negativo, por exemplo: (- 3)3 = (- 3) x (- 3) x (- 3) = - 27.
- Quando a base for negativa e o expoente um número par, o resultado será positivo, por exemplo: (- 2)2 = (- 2) x (- 2) = +4
- Quando o expoente for negativo, inverte-se a base e muda-se o sinal do expoente para positivo, por exemplo: (2)- 4 = (1/2)4 = 1/16
- Nas frações, tanto o numerador quanto o denominador ficam elevados ao expoente, por exemplo: (2/3)3 = (23 / 33) = 8/27
Saiba mais sobre as propriedades da potenciação.
Multiplicação e Divisão de Potências
Na multiplicação das potências de bases iguais, mantém-se a base e soma-se os expoentes:
Na Divisão das potências de bases iguais, mantém-se a base e subtrai-se os expoentes:
(ax) / (ay) = ax-y
(53) / (52) = 53-2 = 51
Quando a base está entre parênteses e há outro expoente fora (potência de potência), mantém-se a base e multiplica-se os expoentes:







 ,
, ,
,
 ,
, ,
, ,
, ,
,
 ,
, ,
,
 ,
, ,
, ,
,
 ,
, ,
,
 ,
, ,
,
 ,
, ,
,
 ,
, ,
,
 ,
, ,
, ,
, ,
, ,
,




![[2^24 + 2^30]/65 = x^x](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgDK0elX3csGKExdHvk67b1Q-I81hW4kQDloEJ6Z6g5HhUzYzLg8gybPtqIEwsIHEC2Z3paYRXuRyfaR3sL_EhVE2HAPAHy28-0QClNe8M0ShpLM0ixm-BRK5sqm-kbnJDAUeqHE9sfNEYP3Y7UbCZ87CtsZ0adG5yAc5kwxCo3LnJCDr33oM98C-XUV4d2/w100/Blog%20do%20Professor%20Janildo%20-%20Copia.png)






.jpg)




















0 Comentários