Apresente o resultado da expressão na forma fracionária:

 

  Grupo Nerd, Matemática e Domínio Público (Telegram)

Apresente o resultado da expressão na forma fracionária:

0,66666... + 0,25252525... – 0,77777...

Há duas opções de resolução para esse exercício: 

a) A primeira é encontrar a fração geratriz de cada dízima periódica e resolver a expressão utilizando as frações. 

b) A segunda opção é encontrar a fração geratriz do resultado da expressão. Para realizarmos menos cálculos, optaremos pela segunda opção, mas vale lembrar que chegaríamos ao mesmo resultado se optássemos pela primeira sugestão. Vamos então realizar a soma inicial através do algoritmo da adição, lembrando que é necessário colocar “vírgula embaixo de vírgula”:

0,66666666...
+0,25252525...
0,91919191...

Desse resultado, vamos subtrair 0,7777777...

0,91919191...
– 0,777777777...
0,14141414...

Vamos agora encontrar a fração geratriz de 0,14141414...

x = 0,14141414...

Multiplicando ambos os lados da equação por 100, temos:

100.x = 14,141414...

Vamos então subtrair dessa equação sua antecedente:

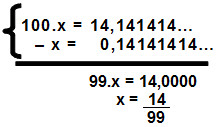
Portanto, a equação tem como resultado a fração 14/99.