InfoEnem |
|
Parecem assuntos completamente diferentes, não é? Porém, em nossa postagem de hoje vamos mostrar como estes assuntos podem ser relacionados. Para isso, vamos explicar de maneira resumida como é feito para determinar a idade de um dinossauro e, em seguida, mostrar como o assunto utilizado é abordado em provas do Enem, utilizando uma questão como exemplo.
Como determinar a idade de um dinossauro?
Para determinar a idade de um fóssil, seja ele um dinossauro ou qualquer outro ser vivo, é utilizado um método denominado datação radioativa. A datação radioativa é baseada no fenômeno da radioatividade, a qual faz com que os átomos percam prótons e/ou nêutrons na forma de radiação, o que causa uma diminuição do número atômico do elemento.
Para os fósseis de seres vivos, normalmente é utilizada a datação através do carbono 14, que perde dois nêutrons por radiação e se transforma em carbono 12. Sabemos que a quantidade de carbono 14 em cada indivíduo é igual, e que esta quantidade cai pela metade após 5730 anos. Esta idade é definida como o tempo de meia vida do carbono 14. Relativamente, o tempo de meia vida do carbono 14 é pequena, sendo possível utilizá-la para determinar a idade de organismos que viveram até 50000 anos atrás. Para se determinar a idade de organismos mais antigos, é necessário utilizar outros elementos, que possuem tempo de meia vida maior.
E como isso é cobrado pelo Enem?
As questões envolvendo a datação de organismos, não só através do carbono 14, mas também de outros elementos, costumam ser muito cobradas nas provas do Enem. Praticamente toda prova de ciências da natureza do Enem carrega uma questão relacionada com o tempo de meia vida de algum elemento.
Para os cálculos que envolvem o tempo de meia vida, são utilizadas duas equações principais. A primeira é mostrada a seguir:

Onde t é o tempo de desintegração do material, P é o tempo de meia vida do elemento medido (para o caso do carbono 14, 5730 anos) e x é o número de meias vidas decorridas pelo material.
Outra equação importante é mostrada abaixo:

Onde m é a massa restante do material radioativo, m0 é a massa inicial presente no organismo e x é o número de meias vidas decorridos.
Com essas duas equações, você pode resolver os exercícios referentes ao tempo de meia vida dos organismos. A seguir, você verá um exercício referente a idade de organismos e o tempo de meia vida, que foi retirado da prova de 2017 do Enem.
“A técnica do carbono-14 permite a datação de fósseis pela medição dos valores de emissão beta desse isótopo presente no fóssil. Para um ser em vida, o máximo são 15 emissões beta/(min g). Após a morte, a quantidade de 14C se reduz pela metade a cada 5730 anos.
A prova do carbono 14. Disponível em http://noticias.terra.com.br. Acesso em 9 nov. 2013 (adaptado)
Considere que um fragmento fóssil de massa igual a 30g foi encontrado em um sítio arqueológico, e a medição de radiação apresentou 6750 emissões beta por hora. A idade desse fóssil, em anos, é”
a) 450
b) 1433
c) 11460
d) 17190
e) 27000
Resposta: Alternativa c!
Com isso, apresentamos em nossa postagem de hoje como é possível determinar a idade de um organismo através da datação por carbono 14 e como este conteúdo é cobrado nas provas do Enem.
O post Como determinar a idade de um dinossauro e o Enem 2020 apareceu primeiro no infoEnem. ESTUDE COM OS MELHORES MATERIAIS PARA O ENEM: CLIQUE AQUI para obter apostilas com mais de 1000 questões do Enem resolvidas e Comentadas Estude com nossos Simulados Online. CLIQUE AQUI para obter a melhor apostila de redação para o Enem Baixe gratuitamente o e-Book: Manual do Sisu / Manual do Prouni
(PUC-Camp-SP) O iodo-125, variedade radioativa do iodo com aplicações medicinais, tem meia-vida de 60 dias. Quantos gramas de iodo-125 restarão após seis meses a partir de uma amostra contendo 2,00 g do radioisótopo?
a) 1,50
b) 0,75
c) 0,66
d) 0,25
e) 0,10
Para realizar esse cálculo, basta realizar os seguintes passos:
⇒ 1o Passo: Calcular o número de meias-vidas.
Utilizar o valor da meia-vida e o tempo decorrido na expressão a seguir:
t = P.x
180 = 60.x
x = 180
60
x = 3
⇒ 2o Passo: Calcular a massa restante.
Utilizar a massa inicial e o número de meias-vidas na seguinte fórmula:
m = mo
2x
m = 2
23
m = 2
8
m = 0,25 g
Cálculo da determinação da meia-vida a partir da massa
Nesse tipo de cálculo, são importantes três dados:
(Unip) Um isótopo de iodo radioativo é muito usado para diagnóstico de doenças de glândula tireoide. A partir de 1 g desse isótopo, após 24 dias, sobra 1/8 g dele. Qual é a meia-vida desse isótopo?
a) 24 dias
b) 8 dias
c) 12 dias
d) 16 dias
e) 4 dias
Para realizar esse cálculo, basta realizar os seguintes passos:
⇒ 1o Passo: Calcular o número de meias-vidas.
Utilizar a massa inicial e o número de meias-vidas:
m = mo
2x
0,125 = 1
2x
2x = 1
0,125
2x = 8
Após realizar a potenciação do número oito para que ele tenha a mesma base dois existente do lado esquerdo da igualdade, temos que:
2x = 23
x = 3
⇒ 2o Passo: Calcular a meia-vida.
Utilizar o valor do número de meias-vidas e o tempo decorrido na expressão a seguir:
t = P.x
24 = P.3
P = 24
3
x = 8 dias
Cálculos envolvendo meia-vida e porcentagem residual
Nesse tipo de cálculo, são importantes dois dados:
Obs.: Como é utilizada a porcentagem, a porcentagem inicial de uma amostra radioativa é sempre igual a 100 %.
Exemplo: (UFPI) Um elemento radioativo tem um isótopo cuja meia-vida é 250 anos. Qual a porcentagem da amostra inicial desse isótopo que existirá após 1000 anos?
Não pare agora... Tem mais depois da publicidade ;)
a) 1,25%
b) 4%
c) 6,25%
d) 12,5%
e) 25%
Para realizar esse cálculo, basta realizar os seguintes passos:
⇒ 1o Passo: Calcular o número de meias-vidas.
Utilizar o tempo decorrido e a meia-vida:
t = P.x
1000 = 250.x
x = 1000
250
x = 4
⇒ 2o Passo: Calcular a porcentagem restante.
Utilizar a massa inicial e o número de meias-vidas:
p = po
2x
p = 100
24
p = 100
16
p = 6,25 %
Cálculo envolvendo meia-vida e idade de um material
Exemplo: (UFPI) A análise de uma amostra de um meteorito indicou que ele contém três átomos de chumbo 82Pb206 para cada átomo de 92U238. Considerando que nenhum 82Pb206 estaria presente na formação do meteorito e que ele é formado pelo decaimento radioativo do 92U238, cuja meia-vida é 4,5 . 109 anos, indique a alternativa correta para a idade do meteorito:
a) 4,5 . 109 anos
b) 9,0 . 109 anos
c) 13,5 . 109 anos
d) 18,0 . 109 anos
e) 22,3 . 109 anos
Para realizar esse cálculo, basta realizar os seguintes passos:
⇒ 1º Passo: Interpretar o enunciado.
O enunciado do exercício informa que há três átomos de chumbo (Pb) para cada átomo de Urânio (U). Assim, se em quatro átomos, ou seja, 100% (um inteiro), apenas um é de urânio, há, portanto, 25% (1 para 4) desse elemento.
⇒ 2º Passo: Calcular o número de meias-vidas.
Utilizar a definição de meia-vida, que é o período em que uma amostra perde metade da sua radiação. Assim, se temos 100% de uma amostra, após uma meia-vida, restarão 50% dela. Após mais uma meia-vida, haverá 25% dela. Em outras palavras, passaram-se duas meias-vidas no decaimento da amostra de 100% para 25%.
⇒ 3º Passo: Determinação da idade do meteorito.
Como o decaimento envolveu a passagem de duas meias-vidas, basta multiplicar esse número pela meia-vida fornecida:
Idade = 2 . 4,5 . 109 anos
Idade = 9. 109 anos
Cálculo envolvendo meia-vida e gráficos
Nesse tipo de situação, os cálculos envolvendo a meia-vida serão realizados a partir de informações retiradas do gráfico e do texto do exercício. Lembre-se de que a meia-vida sempre é determinada de forma simples, com a análise no gráfico, uma vez que se trata do tempo necessário para a redução de 50% (da massa, da fração, etc.) do material radioativo.
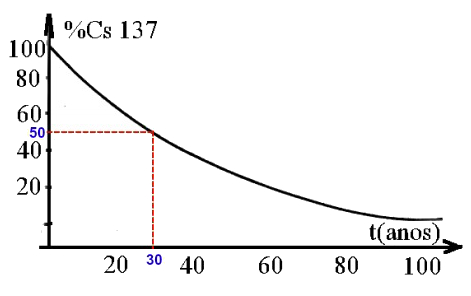
Exemplo: (Unicamp-SP) O césio 137 é um isótopo radioativo produzido artificialmente. O gráfico a seguir indica a porcentagem desse isótopo em função do tempo.
a) Qual a meia-vida desse isótopo?
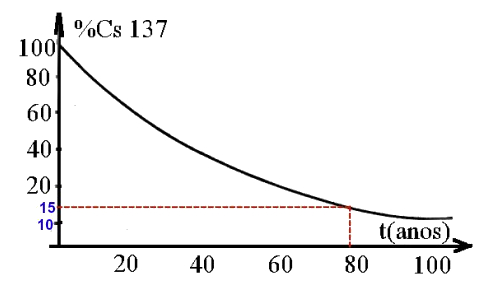
b) Decorridos 80 anos da produção do isótopo, qual a sua radioatividade residual?
Resoluções:
a) Para determinar a meia-vida do césio, basta marcar um ponto entre 60 e 40 no eixo y (onde fica a porcentagem) do gráfico, ir até a curva e, em seguida, descer em direção ao eixo x (onde fica o tempo).
Ao realizar esse procedimento, obtemos que a meia-vida do césio é de aproximadamente 30 anos.
b) A resolução da letra b segue o mesmo padrão descrito na letra a, porém, como há o tempo determinado (80 anos), inciamos a partir do 80 no eixo x, seguimos em direção à curva e, por fim, tracejamos até o eixo y.
Ao realizar esse procedimento, obtemos que a porcentagem restante do césio é de aproximadamente 15%.
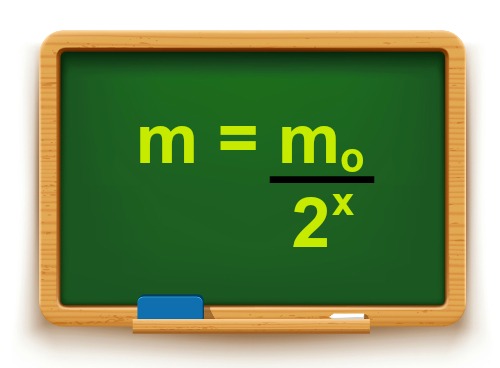 Fórmula utilizada em cálculos que envolvem meia-vida
Publicado por: Diogo Lopes Dias
|



.jpg)









































0 Comentários