Questão 149 - Prova Rosa - ENEM 2016 Primeira Aplicação - Resolvida - Com Vídeo

Questão 149

Resposta D

Vivitem minha página do SCRIBD

 

http://especiais.g1.globo.com/educacao/enem/2016/correcao-provas-enem/#resposta 

Considere apenas o petroleiro todo por enquanto, o paralelepípedo mencionado na questão. 

Desconsidere as placas internas. 

Vamos descobrir o o seu volume. Para isso, basta calcularmos a área da base e multiplicarmos pela altura. Assim:

V = Ab*h
V = 60*10*10
V = 6000 m³ = = > Volume total

Isso significa que todo o compartimento armazena 6000m³ de petróleo. 

Agora vejamos. Considere, agora, as placas lá dentro. Imagine que você está enchendo o petroleiro. Você 

Se temos um buraco em C, irá sair todo o petróleo que preencheria o compartimento C MAIS TODO O PETRÓLEO QUE ESTAVA "EM CIMA" DOS COMPARTIMENTOS A E B. 

No final das contas, restará APENAS o petróleo comportado nos compartimentos A e B. 

O que estava "em cima" deles escapou, vazou pro C e caiu no mar. Ou seja, Tendo todo o volume do petroleiro, só precisamos saber agora quanto CADA COMPARTIMENTO menor comporta. Vamos calcular o volume de um deles (são todos iguais, basta um). Mesma fórmula:

V = Ab.h
V = 20 (60/3) . 10 . 7
V = 1400m³ == > Volume de um dos compartimento que não sofre vazamento. Ora, cada um compartimento comporta 1400 m³, dois (os dois que irão permanecer cheios) comportarão 2 * 1400, ou seja, 2800m³.

Mas essa ainda não é a resposta, pois o que eu quero é o volume total derramado que seria o total menos o que fica nos dois compartimento que não sofrem com o vazamento.

=====================================
RESPOSTA = 6000m³ - 2800m³ = 3200m³
=====================================




3,2.10³ (note que a resposta está em notação científica)

LETRA D

Vivitem minha página do SCRIBD 

Um petroleiro possui reservatório em formato de um paralelepípedo retangular com as dimensões dadas por 60 m x 10 m de base e 10 m de altura. Com o objetivo de minimizar o impacto ambiental de um eventual vazamento, esse reservatório é subdividido em três compartimentos, A, B e C, de mesmo volume, por duas placas de aço retangulares com dimensões de 7 m de altura e 10 m de base, de modo que os compartimentos são interligados, conforme a figura. Assim, caso haja rompimento no casco do reservatório, apenas uma parte de sua carga vazará.

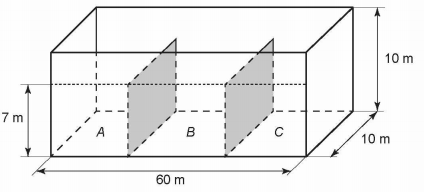
Suponha que ocorra um desastre quando o petroleiro se encontra com sua carga máxima: ele sofre um acidente que ocasiona um furo no fundo do compartimento C.

Para fins de cálculo, considere desprezíveis as espessuras das placas divisórias.

Após o fim do vazamento, o volume de petróleo derramado terá sido de

• a

  1,4 x 103 m3 

• b

  1,8 x 103 m3 

• c

  2.0 x 10 m3 

• d

  3,2 x 103 m3 

• e

  6.0 x 103 m3

Resolução

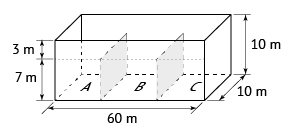
Como o furo ocorreu no fundo do compartimento C, todo o volume de petróleo da parte superior às divisórias (3 · 10 · 60 = 1800 m3), mais o volume do compartimento C que está abaixo da altura da divisória (7 · 10 · 20 = 1400 m3), vazará.

Logo, o volume de petróleo derramado será

3200 m3, ou seja, 3,2 · 103 m3.

Anglo