Do infoenem
Em
artigo recente, estudamos a técnica mais utilizada para determinar o
valor extremo de uma função quadrática, através do vértice de sua função
(veja aqui).
Também realizamos uma discussão sobre a concavidade da parábola,
verificando sua orientação através de seu sinal, implicando em um ponto
de máximo ou mínimo.
Embora seja uma técnica
simples e de rápida aplicação, existem maneiras alternativas para
calcular estes valores. Duas destas técnicas serão apresentadas em nosso
artigo de hoje, cabendo ao aluno decidir qual método utilizará no
decorrer de questões deste tipo.
Para a apresentação destas
técnicas utilizaremos uma função adaptada de uma questão presente no
Enem 2015. O uso de uma função com valores deve tornar o entendimento do
aluno melhor, pois conseguiremos de maneira rápida mostrar que todos os
valores calculados serão iguais! A função que vamos utilizar será:
Com base em nosso artigo
anterior, já podemos concluir que a concavidade da parábola será
voltada para baixo e então calcularemos seu valor máximo, o que era
previsto no enunciado. A primeira técnica que utilizaremos hoje consiste
em aplicar o valor da média aritmética das raízes da equação na mesma,
obtendo neste caso o seu valor máximo. Aplicando este conceito temos
que:
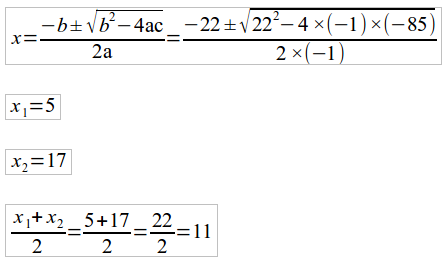
Substituindo o valor da média (11) na função T(x):
Assim, o valor máximo da função é 36.
Podemos ainda utilizar o
conceito de derivada para obter este valor. Embora seja visto em algumas
instituições de ensino médio, a derivada é um recurso
do cálculo diferencial e integral. Como estamos trabalhando com uma
função quadrática, podemos utilizá-la, visto que é de fácil
entendimento. Assim, calcularemos a derivada da função e igualaremos a
zero, obtendo a abscissa do ponto, que nada mais é do que a distância entre este mesmo ponto e o eixo vertical. Então:
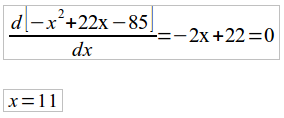
Substituindo na equação de T(x):
Obtemos então o mesmo
valor. Caso o aluno não compreenda o conceito de derivada, não há
problema. Este é um recurso alternativo, e não afetará a sua preparação
para o Enem! Para novamente confirmar as técnicas, vamos obter agora o
valor máximo através de seu vértice:
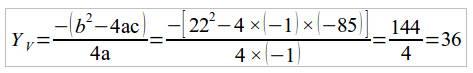
Assim, confirmamos que as três técnicas que apresentamos levam ao
mesmo valor. Cabe agora a cada um definir qual delas possui maior
compreensão, e o melhor jeito de decidir isso é praticando. Portanto,
vamos ao trabalho!
O post Matemática: Técnicas Alternativas de Cálculo de Extremos de Funções apareceu primeiro no infoEnem.
ESTUDE COM OS MELHORES MATERIAIS PARA O ENEM:
Baixe gratuitamente o e-Book: Manual do Enem 2016












































0 Comentários