Tales de Mileto foi um importante filósofo, matemático e astrônomo da Grécia antiga. Embora tenha vivido entre 623 e 548 a.C., Tales é considerado um dos sete sábios do período.
Também
conhecido como pai da geometria descritiva, Tales foi convidado para
determinar a altura de uma das pirâmides do Egito, na qual mesmo não
possuindo nenhum instrumento complexo de medição, conseguiu indicar seu
tamanho exato. Tal feito tornou-se possível através da utilização do Teorema de Tales, que será o alvo de estudo nosso artigo de hoje.
Para
a explicação do teorema de Tales, vamos considerar a seguinte situação:
duas retas transversais (r e r’), que são cortadas por retas paralelas
(a, b e c), assim como é registrado na imagem abaixo:
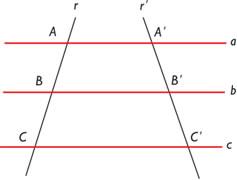
Em
seu teorema, Tales afirmou que a razão entre dois segmentos quaisquer
em uma das retas transversais será igual a razão dos seguimentos
equivalentes em sua outra transversal, ou seja:
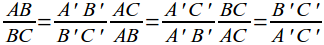
Assim
verificamos que não há uma regra definida para escolha dos segmentos,
sendo necessário somente a utilização do segmento equivalente em outra
transversal. Portanto, podemos escolher os segmentos que nos sejam
convenientes!
Em sua aplicação mais conhecida, Tales utilizou o
seu teorema para determinar a altura de uma das pirâmides do Egito, como
já havíamos mencionado. Para isso, o matemático, de maneira muito
simples, utilizou um pequeno graveto, um instrumento de medição e os
raios solares.
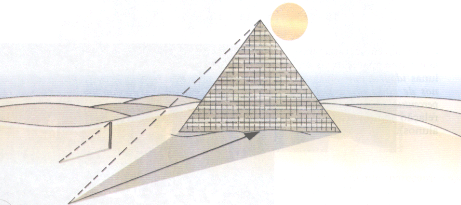
Com
estes materiais, Tales mediu o comprimento do graveto e também a sua
sombra, e após determinar o valor para a sombra da pirâmide, foi
possível determinar a sua altura com exatidão excelente, tudo isso há
cerca de 2.600 anos!
A equação utilizada foi:
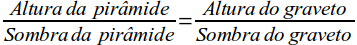
Deste
modo, temos um recurso de fácil aplicação e muito eficaz, que pode ser
usado nas mais diversas situações e transforma-se em um grande aliado na
resolução de exercícios. Até breve!
O post Saiba Tudo Sobre o Teorema de Tales apareceu primeiro no infoEnem.
Postagens
0 Comentários