Em nosso artigo de hoje, daremos início a uma série envolvendo a probabilidade.
A probabilidade teve início desde os tempos mais remotos e até hoje
está presente em grande parcela de eventos de nosso cotidiano,
principalmente em jogos envolvendo cartas e dados, que também irão
aparecer frequentemente em nosso meio.
Por definição, a probabilidade está relacionada com a frequência em que um determinado evento ocorre dentro de um experimento aleatório,
que será o nosso primeiro conceito desta série. Um experimento
aleatório é uma espécie de experimento em que, mesmo realizado sob as
mesmas condições, pode levar a resultados diferentes. O lançamento de um
dado pode ser utilizado para exemplificar esta espécie, pois sob
condições normais, dificilmente obteremos resultados iguais.
Também utilizaremos em nossa sequência o conceito de espaço amostral.
Definimos o espaço amostral como o conjunto de todos os resultados
possíveis de se obter ao realizar um experimento aleatório. Em nossos
artigos, iremos adotar a letra S para
representar o espaço amostral. Seguindo o exemplo de nosso dado, o
espaço amostral obtido será representado pelos números que poderemos
obter em seu lançamento, ou seja:
Podemos
agora então equacionar o nosso conceito de probabilidade. Visto que
trataremos inicialmente de experimentos aleatórios, ambos os eventos
possuem a mesma chance de ocorrer dentro de um mesmo espaço amostral.
Assim, a probabilidade pode ser vista como a divisão entre o número de
ocorrências de um determinado evento dentro de seu espaço amostral.
Então:
Considerando um dado, e suas respectivas faces, ambos os números possuem a mesma probabilidade de ocorrer, cujo valor é:
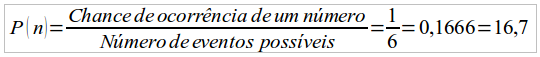
Podemos
verificar que a probabilidade pode ser escrita de diversas maneiras
diferentes, sempre representando o mesmo valor, seja de forma
fracionária ou percentual.
Embora pareça simples, a probabilidade
pode envolver diversas combinações de eventos, o que requer bastante
atenção ao analisar seus problemas. Em breve utilizaremos estes
conceitos iniciais para desenvolver problemas que apresentem uma
complexidade maior, além de abordar novos conceitos desta área.
Que tal resolver exercícios deste assunto e outros em simulados no mesmo modelo do Enem? Então CLIQUE AQUI e cadastre-se na Plataforma de Simulados do infoEnem para começar a praticar!
O post Matemática no Enem – Conceitos Sobre Probabilidade apareceu primeiro no infoEnem.
Postagens
0 Comentários