CEVIANAS:Pontos Notáveis de um Triângulo

Pontos Notáveis de um Triângulo

Kleber Kilhian 

 

Abordaremos aqui os pontos notáveis de um triângulo: Baricentro, Incentro, Circuncentro e Ortocentro. Para uma melhor compreensão do que será estudado, vamos expor algumas definições iniciais:

Cevianas Notáveis

As cevianas aqui estudadas serão: Mediana, Bissetriz Interna e Altura.

O nome ceviana foi dado a esses seguimentos em homenagem ao matemático italiano Giovanni Ceva (1648-1734), que demonstrou teoremas importantes sobre elas.

Definição de Ceviana: é todo seguimento que tem uma das extremidades num vértice qualquer de um triângulo e a outra num ponto qualquer da reta suporte ao lado oposto a esse vértice.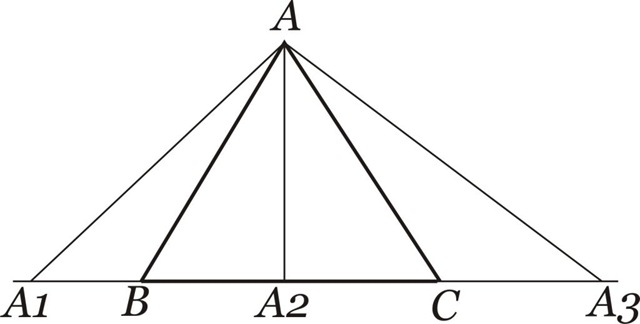

Reta suporte de um seguimento, ou simplesmente suporte de um seguimento, é a reta na qual esse seguimento está contido.

onde r é o suporte de .

Conforme a definição, uma das extremidades da ceviana é um vértice. Podemos dizer que a ceviana é relativa a esse vértice, ou relativa ao lado oposto ao mesmo. A outra extremidade da ceviana é denominada pé. Assim, na figura acima, as cevianas ,  e  são relativas ao vértice A ou também relativa ao lado  e os pontos A₁, A₂ e A₃ são os pés dessas cevianas.

Cada vértice de um triângulo podem conter infinitas cevianas, estas podendo ser internas ou externas.

Dentre essas infinitas cevianas, há três que são muito importantes, por isso são chamadas de notáveis. São elas:

a) Mediana

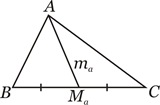
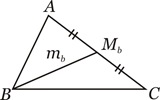
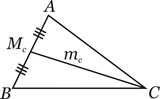
Definição: Mediana é toda ceviana que tem uma das extremidades no ponto médio de um lado.

  

Por convenção, os pontos médios dos lados opostos aos vértices A, B e C são denotados por M_a, M_b e M_c, respectivamente e os comprimentos das medianas relativas aos mesmos são denotados por m_a,m_b e m_C.

b) Bissetriz Interna

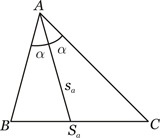
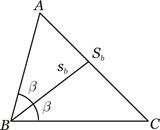
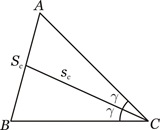
Definição: Bissetriz Interna é toda ceviana que divide um ângulo interno em dois ângulos adjacentes e congruentes.

  

Por convenção, os pés das bissetrizes internas relativas aos vértices A, B e C são denotadas por S_a, S_b e S_c, respectivamente, e os comprimentos das mesmas pors_a, s_b e s_c.

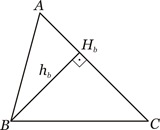
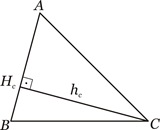
c) Altura

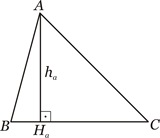
Definição: Altura é toda ceviana perpendicular a um lado ou ao seu suporte.

 

Por convenção, os pés das alturas relativas aos vértices A, B e C são denotados por H_a, H_b e H_c, respectivamente, e os comprimentos dessas alturas por h_a, h_b e h_c.

Pontos Notáveis de um Triângulo

Para qualquer triângulo, valem as seguintes propriedades:

P1) As três medianas concorrem num mesmo ponto;

P2) As três bissetrizes internas concorrem num mesmo ponto;

P3) As retas suportes das três alturas concorrem num mesmo ponto;

P4) As mediatrizes dos lados concorrem num mesmo ponto.

Esses pontos de encontro das cevianas notáveis e das mediatrizes são denominadas pontos notáveis.

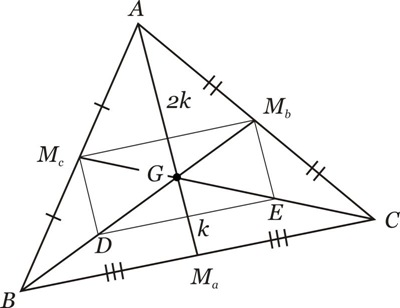
a) Baricentro (G)

As três medianas de um triângulo intersectam-se num mesmo ponto que divide cada mediana em duas partes, sendo que a parte que contém o vértice é o dobro da outra.

Esse ponto é denominado Baricentro do triângulo e é denotado por G.

Demonstração do Baricentro de um Triângulo:

Seja o triângulo abaixo:

Por hipótese, temos:

 ,  e  são medianas.

Por tese, temos:

Demonstração:

Seja X o ponto onde:

Que é o baricentro G que queremos demonstrar. Se considerarmos os pontos médios D e E de  e , temos que , no triângulo ABC:

Se:

 e 

Então:

 e 

E se:

 e 

Então:

 e 

Daí, segue que:

 e 

Logo, M₂M₃DE é paralelogramo.

Então:

Logo, a Mediana , intersecta a mediana  num ponto X tal que:

Tomando-se as Medianas  e  e sendo Y o ponto tal que:

De modo análogo, concluímos que:

De ( I ) e ( III ) vem que X = Y.

Se chamarmos esse ponto X = Y de G e considerarmos ( I ), ( II ) e ( IV ), temos:

e

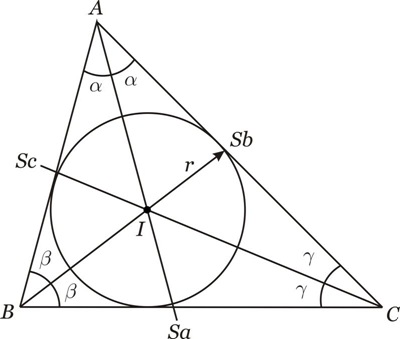
b) Incentro ( I )

As três bissetrizes internas de um triângulo intersectam-se num mesmo ponto. Esse ponto é chamado de Incentro e é denotado por I e se encontra à igual distância dos lados do triângulo.

O Incentro é o centro da circunferência inscrita num triângulo.

Demonstração do Incentro de um Triângulo:

Seja o triângulo abaixo:

Por hipótese temos:

,  e  são bissetrizes internas.

Por tese temos:

e

ds_a = ds_b = ds_c

Demonstração:

Seja I o ponto onde:

Que é o Incentro que queremos demonstrar.

Então:

dS_b = dS_c

e

Logo:

e

dS_a = dS_b = dS_c

c) Circuncentro ( O )

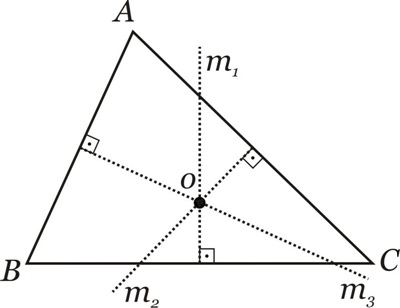
As mediatrizes dos lados de um triângulo intersectam-se num mesmo ponto. Esse ponto é chamado de circuncentro e é denotado por O.

O Circuncentro é o centro da circunferência circunscrita a um triângulo.

O Circuncentro pode ser:

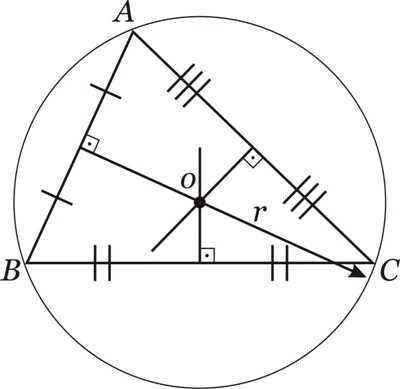
Interno: se o triângulo for acutângulo:

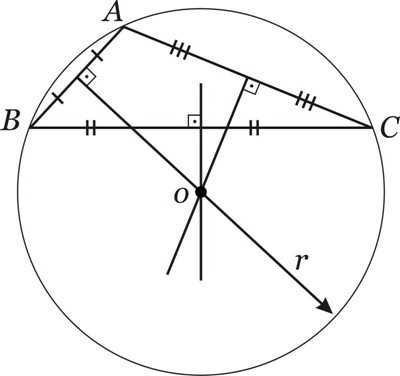
Externo: se o triângulo for obtusângulo:

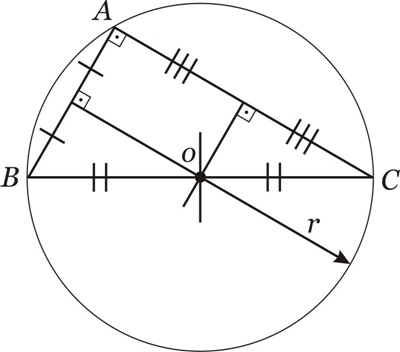
Coincidente: se o triângulo for retângulo:

Demonstração do Circuncentro de um Triângulo:

Seja o triângulo:

Por hipótese, temos:

m₁, m₂ e m₃ são mediatrizes de ,  e .

Por tese, temos:

e

Demonstração:

Seja, então, O o ponto onde:

Se:

Então:

e

Logo:

e

d) Ortocentro (H)

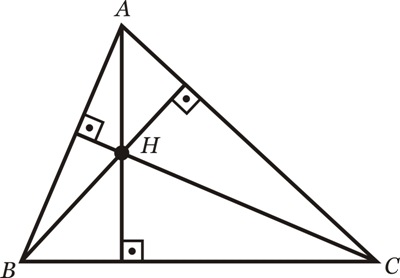
As três retas suportes das alturas de um triângulo intersectam-se num mesmo ponto. Esse ponto é chamado de ortocentro e denotado por H.

O ortocentro pode ser:

Interno: se o triângulo for acutângulo:

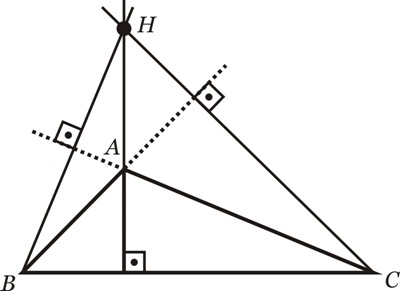
Externo: se o triângulo for obtusângulo:

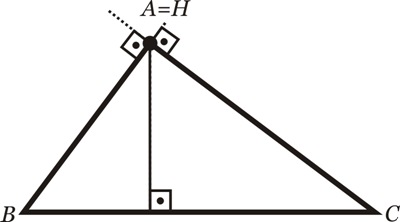
Coincidente: se o triângulo for retângulo:

Demonstração do ortocentro de um triângulo:

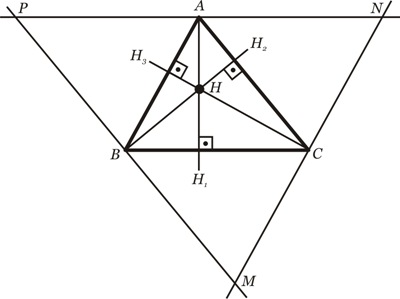
Seja o triângulo:

Pelos vértices A, B e C, traçamos retas paralelas aos lados opostos obtendo o triângulo MNP. Temos então que:

Analisando o triângulo, temos:

APBC é paralelogramo se :

ABCN é paralelogramo se:

Então:

A é o ponto médio de NP ( I )

Em contrapartida:

,  é perpendicular a  ( II )

De ( I ) e ( II ) temos que a reta  é a mediatriz de .

Analogamente, temos:

 é a mediatriz de 

 é a mediatriz de 

Logo, considerando o triângulo MNP, as mediatrizes intersectam-se num ponto H:

Referências:

[1] Fundamento de Matemática Elementar, Vol. 9 – Geometria Plana – Osvaldo Dolce, Ed. Atual
[2] Elementos de Geometria e Desenho Geométrico, Vol. 1 – José Carlos Putnoki, Ed. Scipione

 

in: http://obaricentrodamente.blogspot.com.br/2009/08/pontos-notaveis-de-um-triangulo.html